[행렬식의 엄밀한 정의] ch3. 순열
이전 읽을거리: ch2. 텐서의 성질
다음 읽을거리: ch4. 교대다중선형사상
1. 순열
행렬식은 행렬의 두 행을 바꿀 때 부호가 바뀌게 된다. 이러한 성질을 일반화하기 위해서는 번거롭지만 순열에 대한 논의가 필요하다.
Definition. $k\ge 2$ 에 대해 $\{1,\ldots,k\}$ 의 순열(permutation)이란 정의역과 공역이 $\{1,\ldots,k\}$ 인 일대일대응을 의미한다. $\{1,\ldots,k\}$ 의 모든 순열의 집합을 $S_k$ 라고 쓴다.
다시말해 $\{1,\ldots,k\}$ 의 순열이란 전단사함수 $\{1,\ldots,k\}\to\{1,\ldots,k\}$ 를 의미하며, 이는 k-순서쌍 $(1,2,\ldots,k)$ 의 순서를 섞는 것과 다르지 않다. 이후의 논의들에 따르면 순열의 본질은 사다리게임임을 알 수 있다.
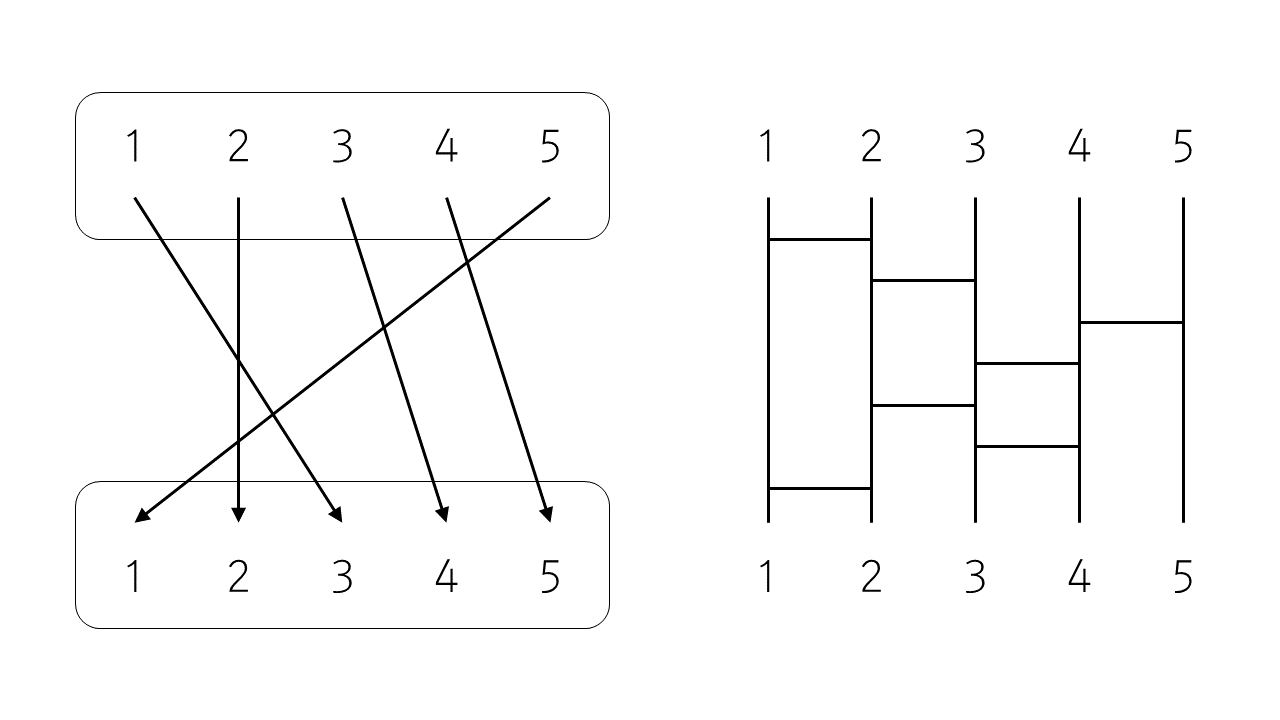
순열을 표기하는 간단한 방법은 순서쌍을 이용하는 것이다. 위 그림의 순열 $\sigma\in S_5$ 를 고지식하게 표현하면 다음과 같다.
$$\begin{align}\sigma(1)&=3\\\sigma(2)&=2\\\sigma(3)&=4\\\sigma(4)&=5\\\sigma(5)&=1\end{align}$$
이 대신에 다음과 같이 표기하는 편이 훨씬 편리하다.
$$\sigma=(3,2,4,5,1)\tag{1}$$
만약 순열이 구체적으로 정해지지 않았다면 다음과 같이 쓰면 된다.
$$\sigma=\Big(\sigma(1),\sigma(2),\sigma(3),\sigma(4),\sigma(5)\Big)$$
사다리게임에서 가로줄은 인접한 두 세로줄을 타고 내려오는 두 대상을 교환하는 역할을 한다. 다음의 정의는 이에 대응하는 순열에 대해 말하고있다.
Definition. $i\in\{1,\ldots,k-1\}$ 에 대해 아래의 두 경우를 제외한 $j\neq i,i+1$ 에 대해 $e_i(j)=j$ 를 만족하는 순열 $e_i\in S_k$ 를 기본순열(elementary permutation)이라고 한다.$$e_i(i)=i+1\quad e_i(i+1)=i$$ $e_i\circ e_i$ 는 항등순열(identity permutation) $\text{id}$ 와 같으므로 $e_i$ 는 자기 자신의 역함수이다.
다음 정리에 따르면 모든 순열은 인접한 두 성분의 교환을 반복하여 얻을 수 있다. 즉, 순열은 사다리게임이다.
Lemma 3.1. 모든 순열은 기본순열의 합성과 같다.
Proof. 임의의 $\sigma\in S_k$ 를 생각하자. 만약 어떤 $i\in\{1,\ldots,k\}$ 가 존재하여 모든 $j\in\{1,\ldots,i\}$ 에 대해 $\sigma(j)=j$ 이면 $\sigma$ 가 첫 $i$ 개 정수를 고정한다고 하자. 이를 만족하는 $i$ 가 존재하지 않으면 편의상 $\sigma$ 가 첫 $0$ 개 정수를 고정한다고 하자.
$\sigma$ 가 첫 $k$ 개 정수를 고정하면 $\sigma$ 는 항등순열이며, 이 경우 아무 기본순열 $e_i$ 에 대해 $\sigma=e_i\circ e_i$ 이므로 본 정리에 부합한다.
본 정리는 귀납법으로 증명할 것이다. 이는 $\sigma$ 가 첫 $i-1$ 개 정수를 고정하면 첫 $i$ 개 정수를 고정하는 $\sigma'$ 와 기본순열의 합성으로 이루어진 어떤 $\pi$ 에 대해 $\sigma=\pi\circ\sigma'$ 가 성립함을 보이면 된다. 이것이 성립한다면 귀납적으로 다음과 같기 때문이다.
$$\sigma=\pi\circ\sigma'=\pi\circ\pi'\circ\sigma''=\cdots=\pi\circ\cdots\circ\pi^{(n)}\circ\text{id}$$
$\sigma$ 가 첫 $i-1$ 개 정수를 고정한다고 하자. $\sigma$ 는 단사이므로 $\sigma(i)$ 는 $1,\ldots,i-1$ 이 아니다. $ \sigma(i)=i$ 인 경우 $\pi=\text{id}$ , $\sigma'=\sigma$ 라고 하면 귀납법의 조건에 부합한다. $\sigma(i)\neq i$ 일 때를 생각하자. $\sigma(i)=l$ 이라고 하고 $\sigma'$ 를 다음과 같이 정의하자.
$$\sigma'=e_i\circ e_{i+1}\circ\cdots\circ e_{l-1}\circ\sigma$$
$\sigma'$ 는 $\sigma$ 의 $1,\ldots,i-1$ 번째 성분에 변화를 주지 않으며 특히 $i$ 번째 성분에 대해 다음이 성립한다.
$$\begin{align}\sigma'(i)&=(e_i\circ e_{i+1}\circ\cdots\circ e_{l-1}\circ\sigma)(i)\\&=(e_i\circ e_{i+1}\circ\cdots\circ e_{l-1})(l)\\&=(e_i\circ e_{i+1}\circ\cdots\circ e_{l-2})(l-1)\\&\vdots\\&=e_i(i+1)\\&=i\end{align}$$
따라서 $\sigma'$ 는 첫 $i$ 개 정수를 고정한다. 여기서 기본순열은 자기 자신의 역함수이므로 다음이 성립한다.
$$\sigma=e_{l-1}\circ\cdots\circ e_i\circ\sigma'$$
$\pi=e_{l-1}\circ\cdots\circ e_i$ 라고 하면 귀납법 조건에 부합하므로 원하는 결과를 얻는다. $\square$
2. 전도
다음의 정의는 순열이 형성하는 '바르지 않은 순서'에 대해 말하고 있다.
Definition. $\sigma\in S_k$ 에 대해 $i<j$ 이고 $\sigma(i)>\sigma(j)$ 인 순서쌍 $(\sigma(i),\sigma(j))$ 를 $\sigma$ 의 전도(inversion)라고 한다. 여기서 $\sigma$ 의 부호(sign)란 $\sigma$ 의 전도 갯수가 홀수이면 $-1$ , 짝수이면 $+1$ 로 정의하고 $\text{sgn }\sigma$ 라고 쓴다.
※ 전도의 올바른 정의는 $(\sigma(i),\sigma(j))$ 가 아닌 $(i,j)$ 로 해야 하지만, 편의상 본 포스팅에서는 정의를 다소 변형하였음.
예를들어 식 (1)에서 $\sigma$ 의 전도는 $(3,2)$ , $(3,1)$ , $(2,1)$ , $(4,1)$ , $(5,1)$ 총 5개, 즉 홀수개이므로 $\text{sgn }\sigma=-1$ 이다.
Theorem 3.2. $\sigma,\;\tau\in S_k$ 에 대해 다음이 성립한다.
(ⅰ) $\sigma$ 가 $m$ 개의 기본순열의 합성과 같으면 $\text{sgn }\sigma=(-1)^m$ 이다.
(ⅱ) $\text{sgn}(\sigma\circ\tau)=(\text{sgn }\sigma)(\text{sgn }\tau)$
(ⅲ) $\text{sgn }\sigma^{-1}=\text{sgn }\sigma$
(ⅳ) $p\neq q$ 에 대해 $\sigma$ 가 $p$ 와 $q$ 를 교환하고 그 외의 모든 정수를 고정하면 $\text{sgn }\sigma=-1$ 이다.
Proof. 본 정리를 증명하기에 앞서 임의의 $\sigma\in S_k$ 와 기본순열 $e_l$ 에 대해 $\text{sgn}(\sigma\circ e_l)=-\text{sgn }\sigma$ 임을 보이자. $\tau=\sigma\circ e_l$ 라고 할때 $\sigma$ 와 $\tau$ 의 전도 갯수는 아래의 수열에서 역순으로 쓰인 두 정수쌍의 갯수이다.
$$\sigma=\Big(\sigma(1),\ldots,\sigma(l-1),\textcolor{red}{\sigma(l)},\textcolor{blue}{\sigma(l+1)},\sigma(l+2),\ldots,\sigma(k)\Big)\tag{2}$$
$$\begin{align}\tau&=\Big(\tau(1),\ldots,\tau(l-1),\textcolor{green}{\tau(l)},\textcolor{green}{\tau(l+1)},\tau(l+2),\ldots,\tau(k)\Big)\\&=\Big(\sigma(1),\ldots,\sigma(l-1),\textcolor{blue}{\sigma(l+1)},\textcolor{red}{\sigma(l)},\sigma(l+2),\ldots,\sigma(k)\Big)\end{align}\tag{3}$$
$\{1,\ldots,k\}$ 의 두 정수 $p\neq q$ 에 대해 두 수열에서 $\sigma(p),\;\sigma(q)$ 의 위치를 비교하자.
$p$ 와 $q$ 모두 $l$ , $l+1$ 이 아닌경우 $\sigma(p),\;\sigma(q)$ 의 위치는 두 수열에서 동일하게 나타난다. 이 경우 $(\sigma(p),\sigma(q))$ 가 전도일 필요충분조건은 $(\tau(p),\tau(q))$ 가 전도인 것이다.
$p$ 또는 $q$ 둘 중에 하나만, 예를들어 $p$ 가 $l$ 또는 $l+1$ 이고 $q$ 는 $l$ , $l+1$ 가 아닐 때를 생각하자. 이 경우 $\sigma(q)$ 는 두 수열에서 동일한 위치에 나타나지만 $\sigma(p)$ 는 두 수열에서 서로 다른 위치에 나타나게 된다. 그럼에도 불구하고 두 수열에서 $\sigma(p),\;\sigma(q)$ 가 나타나는 순서는 교차되지 않으므로, 마찬가지로 $(\sigma(p),\;\sigma(q))$ 가 전도일 필요충분조건은 $(\tau(p),\tau(q))$ 가 전도인 것이다.
여기까지 $\sigma$ 와 $\tau$ 의 전도 갯수는 다르지 않다. 하지만 $(\sigma(l),\sigma(l+1))$ 이 전도이면 $(\tau(l),\tau(l+1))$ 은 전도가 아니며, 반대로 $(\sigma(l),\sigma(l+1))$ 아 전도가 아니면 $(\tau(l),\tau(l+1))$ 은 전도이다. 결과적으로 $\sigma$ 와 $\tau$ 의 전도 갯수는 단 하나가 차이나므로 원하는 결과를 얻는다. 이어서 본 정리를 증명하자.
(ⅰ) 위 결론에 따르면 어떤 순열에 기본순열을 $m$ 번 합성하면 부호가 $m$ 번 바뀌게 된다. $\text{id}=e_i\circ e_i$ , 즉 $\text{sgn id}=1$ 이므로 기본순열 $m$ 개의 합성은 1에서 부호를 $m$ 번 바꾸게 되어 원하는 결과를 얻는다.
(ⅱ) $\sigma,\;\tau$ 가 각각 $m,\;n$ 개의 기본순열의 합성과 같다고 하면 (ⅰ)에 따라 다음이 성립한다.
$$\begin{align}\text{sgn}(\sigma\circ\tau)&=(-1)^{m+n}=(-1)^m(-1)^n\\&=(\text{sgn }\sigma)(\text{sgn }\tau)\end{align}$$
(ⅲ) $\text{sgn id}=1$ 이며 $\sigma^{-1}\circ\sigma=\text{id}$ 이므로 (ⅱ)에 따라 $(\text{sgn }\sigma^{-1})(\text{sgn }\sigma)=1$ 을 얻는다. 따라서 $\text{sgn }\sigma^{-1}$ 와 $\text{sgn }\sigma$ 는 부호가 같아야하므로 원하는 결과를 얻는다.
(ⅳ) 이를 증명하는 것은 그저 전도 갯수를 세면 된다. $p$ 와 $q$ 만 교환하는 수열 $\sigma$ 는 아래와 같다. (편의상 $p<q$ 라고 하자)
$$\sigma=(1,\ldots,p-1,\textcolor{red}{q},p+1,\ldots,q-1,\textcolor{red}{p},q+1,\ldots,k)$$
여기서 $p$ 또는 $q$ 를 포함하지 않는 순서쌍은 전도가 아님이 자명하다. $q$ 를 포함하는 전도는 아래와 같다.
$$(q,p+1),\;(q,p+2),\;\ldots,\;(q,q-1)$$
$p$ 를 포함하는 전도는 아래와 같다.
$$(p+1,p),\;(p+2,p),\;\ldots,\;(q-1,p)$$
여기까지의 전도의 수는 짝수이며, 마지막으로 $(q,p)$ 를 세면 $\sigma$ 의 전도 갯수가 홀수이므로 원하는 결과를 얻는다. $\square$
읽어주셔서 감사합니다.
References)
[1] 스티븐 H, 프리드버그. (2020). 프리드버그 선형대수학 (한빛수학교재연구소 옮김). 한빛아카데미.
[2] 김홍종. (2020). 미적분학 1+. 서울대학교출판문화원.
[3] James R. Munkres. (1991). Analysis on manifolds. CRC press.
이전 읽을거리: ch2. 텐서의 성질
다음 읽을거리: ch4. 교대다중선형사상
'수학 > 선형대수학' 카테고리의 다른 글
| [행렬식의 엄밀한 정의] ch5. 교대텐서의 성질 (0) | 2022.10.30 |
|---|---|
| [행렬식의 엄밀한 정의] ch4. 교대다중선형사상 (0) | 2022.10.29 |
| [행렬식의 엄밀한 정의] ch2. 텐서의 성질 (0) | 2022.10.29 |
| [행렬식의 엄밀한 정의] ch1. 다중선형사상 (2) | 2022.10.28 |
| [행렬식의 엄밀한 정의] ch0. 행렬식의 귀납적 정의 (0) | 2022.10.28 |

댓글