[FTC의 엄밀한 증명] ch22. 평균값 정리
이전 읽을거리 : [FTC의 엄밀한 증명] ch21. 페르마의 임계점 정리
다음 읽을거리 : [FTC의 엄밀한 증명] ch23. 리만 적분
본 포스팅은 'Stephen Abbott, 해석학 첫걸음(2판)'을 공부하며 작성하였습니다.
24. 평균값 정리
평균값 정리의 기하학적 의미는 다음과 같다. 구간 $[a,b]$ 에서 미분가능한 함수 $f$ 에 대해 그래프의 양 끝점 $(a,f(a))$ 와 $(b,f(b))$ 를 잇는 직선의 기울기와 같은 접선이 반드시 존재한다. 간단히 말하면 어떤 점 $c\in(a,b)$ 에 대해 다음이 성립한다.
$$Df(c)=\frac{f(b)-f(a)}{b-a}$$
이러한 관찰은 얼핏보면 지극히 당연하게 느껴지기도 한다. 그러나 이는 사잇값 정리와 같이 해석학이 쌓아올린 거대한 피라미드 꼭대기의 돌과 같은 것이다. 즉 평균값 정리는 지금까지 흘린 땀과 잉크에 대한 보상이다.
나중에 알게 되겠지만 평균값 정리는 미분과 관련된 주요한 정리의 증명과정에 빈번히 쓰이는, 매우 값진 결과이다.
다음의 정리는 평균값 정리의 특수한 경우로, 평균값 정리를 증명하는데 쓰인다.
롤의 정리 (Rolle's theorem)
함수 $f:A\to\mathbb{R}$ 이 $[a,b]\subset A$ 에서 연속이고 $(a,b)$ 에서 미분가능하며 $f(a)=f(b)$ 이면 어떤 $c\in(a,b)$ 가 존재하여 $Df(c)=0$ 이 성립한다.
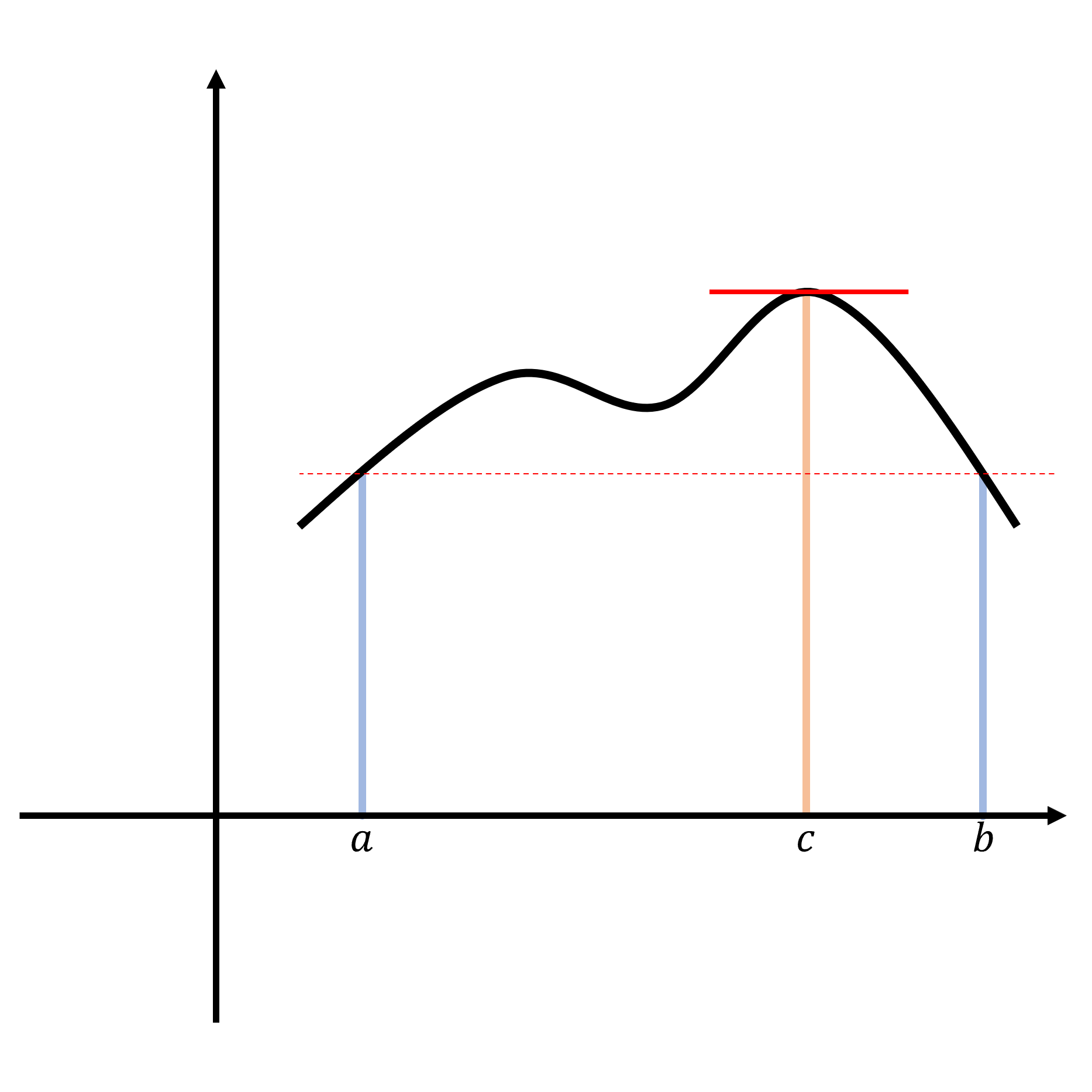
proof)
$f$ 가 콤팩트 집합 $[a,b]$ 에서 연속이므로 $f\big([a,b]\big)$ 는 최댓값과 최솟값을 가진다.
$c=a$ 또는 $c=b$ 에 대해 $f(c)$ 가 $f\big([a,b]\big)$ 의 최댓값과 최솟값이라고 가정하자. $f(c)=f(a)$ 이므로 임의의 $x\in[a,b]$ 에 대해 $f(a)\ge f(x)$ 이고 $f(a)\le f(x)$ 이므로 $f(a)=f(x)$ 이다. 이 경우 임의의 $c\in(a,b)$ 에 대해 $Df(c)=0$ 이므로 정리가 자명하게 성립한다.
어떤 $c\in(a,b)$ 에 대해 $f(c)\neq f(a)$ 가 $f\big([a,b]\big)$ 의 최댓값 또는 최솟값이라고 가정하자. $(a,b)$ 는 열린 집합이므로 어떤 $\epsilon>0$ 이 존재하여 $B_\epsilon(c)\subset(a,b)\subset A$ 가 성립한다. 따라서 $c$ 는 $f$ 의 극점이며 $c\in A^\circ$ 이다. 이 때 $f$ 는 $c\in(a,b)$ 에서 미분가능하므로 페르마의 임계점 정리에 따라 $Df(c)=0$ 을 얻는다. $\square$
롤의 정리의 따름정리로 평균값 정리를 쉽게 얻을 수 있다.
평균값 정리 (mean value theorem)
함수 $f:A\to\mathbb{R}$ 이 $[a,b]\subset A$ 에서 연속이고 $(a,b)$ 에서 미분가능하면 다음을 만족하는 $c\in(a,b)$ 가 존재한다.$$Df(c)=\frac{f(b)-f(a)}{b-a}$$

proof)
다음의 함수 $d:A\to\mathbb{R}$ 을 생각하자.
$$d(x)=f(x)-\left(\frac{f(b)-f(a)}{b-a}(x-a)+f(a)\right)$$
이는 각 $x$ 에서 $(a,f(a))$ 와 $(b,f(b))$ 를 잇는 직선과 $f(x)$ 의 차이에 대한 함수이다. 함수 $d$ 는 $[a,b]$ 에서 연속이며 $(a,b)$ 에서 미분가능하며 $d(a)=d(b)=0$ 이다. 롤의 정리에 따라 어떤 $c\in(a,b)$ 에 대해 다음이 성립한다.
$$\begin{align}0&=Dg(c)\\&=Df(c)-\frac{f(b)-f(a)}{b-a}\end{align}$$
$$\therefore Df(c)=\frac{f(b)-f(a)}{b-a}\tag*{$\square$}$$
평균값 정리를 한번 더 일반화하면 다음의 정리를 얻을 수 있다.
코시 평균값 정리 (generalized mean value theorem)
함수 $f,g:A\to\mathbb{R}$ 이 $[a,b]\subset A$ 에서 연속이고 $(a,b)$ 에서 미분가능하면 다음을 만족하는 $c\in(a,b)$ 가 존재한다.$$\big(f(b)-f(a)\big)Dg(c)=\big(g(b)-g(a)\big)Df(c)$$
※ 위 정리에서 $g(x)=x$ 이라고 하면 평균값 정리이므로, 평균값 정리는 코시 평균값 정리의 특수한 경우이다.
proof)
다음의 함수 $h:A\to\mathbb{R}$ 을 생각하자.
$$h(x)=\big(f(b)-f(a)\big)g(x)-\big(g(b)-g(a)\big)f(x)$$
여기서 다음이 성립한다.
$$\begin{align}h(a)&=\big(f(b)-f(a)\big)g(a)-\big(g(b)-g(a)\big)f(a)\\&=f(b)g(a)-f(a)g(b)\end{align}$$
$$\begin{align}h(b)&=\big(f(b)-f(a)\big)g(a)-\big(g(b)-g(a)\big)f(a)\\&=f(b)g(a)-f(a)g(b)\end{align}$$
$$\therefore h(a)=h(b)$$
$h$ 는 $[a,b]$ 에서 연속이며 $(a,b)$ 에서 미분가능하므로 롤의 정리에 따라 어떤 $c\in(a,b)$ 에 대해 다음이 성립한다.
$$\begin{align}0&=Dh(c)\\&=\big(f(b)-f(a)\big)Dg(c)-\big(g(b)-g(a)\big)Df(c)\end{align}$$
$$\therefore\big(f(b)-f(a)\big)Dg(c)=\big(g(b)-g(a)\big)Df(c)$$
따라서 원하는 결과를 얻는다. $\square$
읽어주셔서 감사합니다.
이전 읽을거리 : [FTC의 엄밀한 증명] ch21. 페르마의 임계점 정리
다음 읽을거리 : [FTC의 엄밀한 증명] ch23. 리만 적분
'수학 > 해석학' 카테고리의 다른 글
| [FTC의 엄밀한 증명] ch24. 리만 적분의 성질 1 (0) | 2022.03.24 |
|---|---|
| [FTC의 엄밀한 증명] ch23. 리만 적분 (0) | 2022.03.23 |
| [FTC의 엄밀한 증명] ch21. 페르마의 임계점 정리 (0) | 2022.03.14 |
| [FTC의 엄밀한 증명] ch20. 미분의 성질 (0) | 2022.03.09 |
| [FTC의 엄밀한 증명] ch19. 연쇄법칙 (0) | 2022.03.09 |

댓글