[FTC의 엄밀한 증명] ch2. 완비성 공리

  이전 읽을거리 : [FTC의 엄밀한 증명] ch1. 실수의 정의

  다음 읽을거리 :

  [FTC의 엄밀한 증명] ch3. 수열의 극한

  [직선과 실수] ch1. 순서체의 엄밀한 정의

 

 

  본 포스팅은 'Stephen Abbott, 해석학 첫걸음(2판)'을 공부하며 작성하였습니다.

 

※ 본 포스팅은 PC 환경에서 보기를 권장합니다.

 

 

2. 완비성 공리

 

  완비성 공리를 대뜸 공개하자면 다음과 같다.

 

완비성 공리 (Axiom of Completeness)
  공집합이 아니고 위로 유계인 (실수 집합의) 부분집합은 항상 상한을 갖는다.

 

  이를 처음 본다면 '위로 유계', '상한'과 같이 낯선 단어때문에 알아볼 수가 없을 것이다. 차근차근 그 정의를 확인하자.

 

정의)  어떤 $b\in \mathbb{R}$ 이 존재하여 모든 $a\in A$ 에 대해 $a\le b$ 를 만족하면 집합 $A\subset \mathbb{R}$ 은 위로 유계(bounded above)라고 정의한다. 이때 $b$ 는 $A$ 의 상계(upper bound)라고 한다.

 

  친숙한 비유를 들자면, 상계란 집합의 '뚜껑'이며, 뚜껑이 존재하는 집합을 가리켜 위로 유계라고 할 수 있다.

 

  유의할 점은 상계가 그 집합 안에 꼭 포함되어야할 필요는 없다는 것이다. 그리고 상계는 단 하나일 필요도 없다. 예로서 닫힌 구간 $[0,3]$ 은 $3,4,5$ 등이 그 상계가 될 수 있으므로, 이 집합은 위로 유계이다.

 

  앞서 말했듯이 위로 유계인 집합의 상한은 하나가 아닐수도 있다. 똑바로 말하면, 상한은 존재한다면 무수히 많이 존재한다. 여러가지 상한들 중에서 우리가 원하는 상한은 단 하나이다.

 

정의)  실수 $s$ 가 다음 두 조건을 만족하면 $s$ 를 집합 $A\subset \mathbb{R}$ 의 최소상계(least upper bound) 또는 상한(supremum)이라고 하며, $s=\text{sup}A$ 라고 표기한다.
  (ⅰ) $s$ 는 $A$ 의 상계이다.
  (ⅱ) $A$ 의 임의의 상계 $b$ 에 대하여 $s\le b$ 이다.

 

  다시 비유를 들자면, 상한은 뚜껑(상계)중에 가장 꽉 눌러잠근 뚜껑이라고 할 수 있다.

 

  어느 집합에 상한이 존재한다면, 오직 하나만 존재한다. 어떤 집합의 임의의 두 상한 $s_1,s_2$ 가 존재한다고 가정하자. 상한의 첫 번째 조건에 따라 $s_1,s_2$ 는 상계이다. 상한의 두 번째 조건에 따라 $s_1\le s_2$ 이며 $s_2\le s_1$ 이다. 즉 $s_1=s_2$ 이므로 상한은 유일하다.

 

위와 아래로 유계인 집합 A

 

  다시 완비성 공리로 돌아오자. 공집합이 아닌 위로 유계인 집합 $A\subset \mathbb{R}$ 은 항상 상한을 가진다고 했다. 다시말해 실수의 부분집합이라면 뚜껑이 있는 집합은 가장 꽉 눌러잠근 뚜껑이 존재한다는 것이다. 이러한 성질 덕분에 실수는 유리수와 구분된다고 수학자들은 말한다. 헌데...

 

  여기서 한 번 의심해 볼 필요가 있다. 위로 유계인 집합은, 굳이 실수의 부분집합이 아니더라도 당연히 상한을 가져야 하는 것이 아닌가? 만약 상한을 가지지 않는다면 그건 어떤 모습인걸까?

 

  유리수 세계에서는 완비성 공리가 적용되지 못한다. 다음과 같은 유리수의 부분집합을 생각하자.

$$S=\{r\in \mathbb{Q}:r^2<2\}$$

  $S$ 는 제곱해서 2보다 작은 수이므로, $S$ 의 모든 원소는 $\sqrt{2}$ 보다 작다. $S$ 의 유리수인 상계는 얼마든지 찾을 수 있지만, 유리수인 상한이 존재할까?

$$\sqrt{2}=1.4142135623730950488016887242...$$

  $15/10$ , $142/100$ , $1415/1000$ 등등.. 점점 더 작은 상계를 찾아볼 수는 있다. 그러나 가장 작은 상계라는 것은 존재하지 않을 것이다. 나중에 증명하겠지만, 서로 다른 두 수 사이에는 반드시 유리수가 존재한다. ($\sqrt{2}$ 가 아닌) 유리수인 상한이 존재한다고 우겨본들, $\sqrt{2}$ 와 그 상한 사이에는 또다른 유리수 상계가 존재한다는 것이다.(그럼 상한이 상한이 아니게 된다)

 

  정리하자면 유리수의 부분집합이지만 유리수인 상한이 존재하지 않는 집합이 존재한다. 따라서 완비성 공리는 유리수에서 성립하지 않는 성질이며, 유리수와 실수를 구분짓는 특성이라고 말할 수 있다. 그러나 명심하자. 완비성 공리는 고작 유리수와 실수를 구분짓기 위해서가 아닌, 실수를 모든 길이에 대응시킨다는 원대를 목표를 갖고 태어났다. 이에 대해서는 아래에서 확인하자.

 

  상한에 관한 정의의 대칭된 형태로 다음과 같은 정의가 필요할 때도 있다.

 

정의)  어떤 $b\in \mathbb{R}$ 이 존재하여 모든 $a\in A$ 에 대해 $b\le a$ 를 만족하면 집합 $A\subset \mathbb{R}$ 은 아래로 유계(bounded below)라고 정의한다. 이때 $b$ 는 $A$ 의 하계(lower bound)라고 한다.

 

정의)  실수 $s$ 가 다음 두 조건을 만족하면 $s$ 를 집합 $A\subset \mathbb{R}$ 의 최대하계(greatest lower bound) 또는 하한(infimum)이라고 하며, $s=\text{inf}A$ 라고 표기한다.
  (ⅰ) $s$ 는 $A$ 의 하계이다.
  (ⅱ) $A$ 의 임의의 하계 $b$ 에 대하여 $b\le s$ 이다.

 

 

2.1. 완비성 공리의 따름정리

 

  완비성 공리는 자세히 보면 반쪽만 설명해놓은 공리이다. 완비성 공리에는 공집합이 아닌 아래로 유계인 집합이 하한을 가진다고 명시하지는 않았다. 그 이유는, 상한에 대한 설명으로 이러한 사실을 이끌어낼 수 있기 때문이다. 다음을 확인하자.

 

정리 2.1-1)  공집합이 아니고 아래로 유계인 (실수 집합의) 부분집합은 항상 하한을 갖는다.

 

proof)

  공집합이 아니고 아래로 유계인 집합 $A\subset \mathbb{R}$ 을 생각하자. $A$ 는 아래로 유계이므로 하계가 존재한다. 다음과 같은 집합을 생각하자.

$$B=\{b\in \mathbb{R}:\mathrm{\forall }a\in A,b\le a\}$$

  즉, $B$ 는 $A$ 의 하계들의 집합이다. $B$ 의 모든 원소는 $A$ 의 하계이므로, $A$ 의 임의의 원소는 $B$ 의 모든 원소보다 크다. 따라서 $A$ 의 임의의 원소는 $B$ 의 상계이다. 그러므로 $B$ 는 위로 유계인 집합이므로, 완비성 공리에 따라 $B$ 는 상한 $\text{sup}B$ 가 존재한다.

  $A$ 의 모든 원소는 $B$ 의 상계이며 $\text{sup}B$ 는 $B$ 의 최소상계이므로 $A$ 의 임의의 원소 $a$ 에 대하여 $\text{sup}B\le a$ 가 성립한다. 따라서 $\text{sup}B$ 는 $A$ 의 하계이다. $\text{sup}B$ 는 $B$ 의 상계이므로 $B$ 의 임의의 원소 $b$ 에 대하여 $b\le \text{sup}B$ 가 성립한다. 즉, $\text{sup}B$ 는 $A$ 의 하계이며 $A$ 의 모든 하계보다 크거나 같다. 따라서 $\text{sup}B$ 는 $A$ 의 최대하계, 하한이다.   $◻$

 

 

  완비성 공리의 위대한 점은 바로 해석학을 엄밀한 논증의 영역으로 밀어넣는다는 점이다. 예를 들어, 다음과 같이 너무나 당연한 명제도 증명이 가능하다.

 

아르키메데스 성질 (Archimedean Property)
  임의의 두 양수 $a,b>0$ 에 대해 어떤 자연수 $n\in \mathbb{N}$ 이 존재하여 $a<nb$ 가 성립한다.

 

  아르키메데스 성질은 다시말해 아무리 작은 양수라도 몇 번을 더하면 아무리 큰 수보다 더 크게 만들 수 있다는 말이다. 이는 실수계에 '무한소'와 같은 존재가 없음을 시사한다.

 

proof)

  아르키메데스의 성질의 증명은 자연수집합 $\mathbb{N}$ 이 $\mathbb{R}$ 에서 위로 유계가 아님을 보이며 시작한다. 모순을 보이기 위해 $\mathbb{N}$ 이 위로 유계라고 가정하자. 완비성 공리에 따라 $\mathbb{N}$ 의 상한(최소상계) $\alpha =\text{sup}\mathbb{N}$ 이 존재한다. $\alpha -1$ 은 $\mathbb{N}$ 의 상계가 될 수 없으므로, $\alpha -1<m$ 을 만족하는 자연수 $m\in \mathbb{N}$ 이 존재한다. 이때 $\alpha <m+1$ 이며 $m+1$ 은 $\mathbb{N}$ 의 원소이므로 $\alpha$ 가 $\mathbb{N}$ 의 상한이라는 가정에 모순이다. 따라서 $\mathbb{N}$ 은 위로 유계가 아니다.

  $\mathbb{N}$ 이 위로 유계였다면 임의의 자연수 $m$ 에 대하여 $m\le s$ 이도록 하는 실수 $s\in \mathbb{R}$ 이 존재하여야 한다. 그러나 $\mathbb{N}$ 는 위로 유계가 아니므로, 임의의 실수 $r$ 에 대하여 $r<n$ 이도록 하는 자연수 $n\in \mathbb{N}$ 이 존재한다. 이를 논리기호로 설명하면 다음과 같다.

$$\begin{array}{rl}\sim (\mathrm{\forall }n\in \mathbb{N},\mathrm{\exists }r\in \mathbb{R}& \text{s.t.}n\le r)\\ \equiv \mathrm{\exists }n\in \mathbb{N},\mathrm{\forall }r\in \mathbb{R}& \text{s.t.}r<n\end{array}$$

  임의의 두 양수 $a,b\in \mathbb{R}$ 에 대하여, $a/b<n$ 을 만족하는 자연수 $n$ 이 존재하므로 $a<nb$ 이다. 따라서 원하는 결과를 얻는다.   $◻$

 

 

  아래의 따름정리는 해석학 한정, 아르키메데스 성질의 존재 의의라고 해도 무방하다. 앞으로 자주 애용하게 될 정리이다.

 

아르키메데스 성질의 따름정리)  임의의 양수 $a>0$ 에 대해 어떤 자연수 $n\in \mathbb{N}$ 이 존재하여 $\frac{1}{n}<a$ 가 성립한다.

 

proof)

  아르키메데스 성질에 따르면 임의의 양수 $a>0$ 에 대하여 $1<na$ 가 성립하도록 하는 자연수 $n\in \mathbb{N}$ 이 존재한다. $\frac{1}{n}<a$ 이므로 원하는 결과를 얻는다.   $◻$

 

 

  이 따름정리는 이처럼 증명이 너무 짧고 단순하므로, 아르키메데스 성질 그 자체와 달라보이는 구석이 거의 없어보일 정도이다. 앞으로 '아르키메데스 성질'이라 하면 그 따름정리도 같이 가리키는 것이라고 하자.

 

  이쯤에서 유리수도 충분히 훌륭한 수체계라는 것을 상기시키자. 괜히 그리스인들이 길이를 나타내기 위해 유리수로 만족했던 것이 아니다. 유리수도 빽빽할만큼 빽빽한 집합이다. 빽빽한 집합이라는 것을 수학적으로 표현해보자.

 

정의)  집합 $S\subset \mathbb{R}$ 을 생각하자. 임의의 두 실수 $a<b$ 에 대해 어떤 $s\in S$ 가 존재하여 $a<s<b$ 가 성립하면 $S$ 는 $\mathbb{R}$ 에서 조밀하다고 한다.

 

※ 사실 조밀성의 엄밀한 정의에는 위상의 개념이 나타난다. 위의 정의는 해석학 공부를 막 시작한 사람이 볼 수 있도록 변형한 동치 명제이다.

 

  다시말해 $\mathbb{R}$ 에서 조밀한 집합 $S$ 는 아무리 좁은 실수구간에서도 $S$ 의 원소가 발견된다. 조금만 더 생각해본다면 그 좁은 실수구간 안에 $S$ 의 원소가 무한히 존재한다는 것을 알 수 있다. 다음의 정리에 따르면, 아무리 좁은 실수 구간을 잡아도 그 안에 유리수가 무한히 존재한다.

 

정리 2.1-2)  유리수집합 $\mathbb{Q}$ 는 $\mathbb{R}$ 에서 조밀하다.

 

proof)

  임의의 두 실수 $a<b$ 를 생각하자. 두 실수 사이에는 $b-a$ 만큼의 '틈'이 존재하는데, 아르키메데스 성질에 따르면 이 틈이 아무리 작더라도 유한번 더하여 얼마든지 크게 만들 수 있다. 이를테면 $1<n(b-a)$ 가 성립하도록 하는 자연수 $n\in \mathbb{N}$ 이 존재한다. 이때 $na+1<nb$ 가 성립하므로 $na$ 와 $nb$ 사이에는 정수가 적어도 하나 이상 들어갈 수 있는 공간이 있다.

  $na$ 보다 크면서 정수중에는 제일 작은 정수 $m$ 을 선택하자. 다음이 성립한다.

$$m-1\le na<m$$

  이때 $m-1\le na$ 의 양변에 1을 더하여 다음의 부등식을 얻을 수 있다.

$$m\le na+1<nb$$

  $na<m$ 이 되도록 정수 $m$ 을 선택하였으므로 다음이 성립한다.

$$na<m<nb$$

$$\therefore a<\frac{m}{n}<b$$

  따라서 $a$ 와 $b$ 사이에는 유리수 $\frac{m}{n}$ 이 존재한다. 처음에 두 실수 $a,b$ 를 임의로 선택하였으므로 $\mathbb{Q}$ 는 $\mathbb{R}$ 에서 조밀하다.   $◻$

 

 

※ 유리수집합 $\mathbb{Q}$ 뿐 아니라 무리수집합 $\mathbb{I}$ 도 $\mathbb{R}$ 에서 조밀하다. 그렇게 중요한 사실은 아니므로 만약 궁금한 분이 있다면 직접 증명해보길 바란다. 유리수와 무리수를 더하면 항상 무리수임을 밝히면 그 뒤는 매우 쉽다.

 

  한가지 당연한 말을 하자면, $\mathbb{R}$ 은 $\mathbb{R}$ 에서 조밀하다. 임의의 두 실수 $x,y$ 사이에 $\frac{x+y}{2}$ 가 있기 때문이다.

 

  다음은 다소 낯설게 느껴질 수 있는 정리이다. 그러나 $\sqrt{2}=1.414213562...$ 와 같은 실수의 소수전개의 존재성을 보장해주는 중요한 정리이며, 해석학의 중요한 증명들에서 강력한 힘을 발휘하는 정리이다.

 

축소구간성질 (Nested Interval Property)
  자연수를 첨자로 갖는 닫힌 구간열 $I_n=[a_n,b_n]=\{x\in \mathbb{R}:a_n\le x\le b_n\}$ 을 생각하자. 이때 임의의 자연수 $n$ 에 대하여, $I_n$ 이 $I_{n+1}$ 을 포함한다고 하자.
$$I_1\supset I_2\supset I_3\supset I_4\supset \cdots$$  이와 같이 닫힌 구간열은 공집합이 아닌 교집합을 가진다. 즉, 다음이 성립한다.
$$\bigcap _{n=1}^{\mathrm{\infty }}{I}_n\ne \varnothing$$

 

그림 출처 - 위키피디아

 

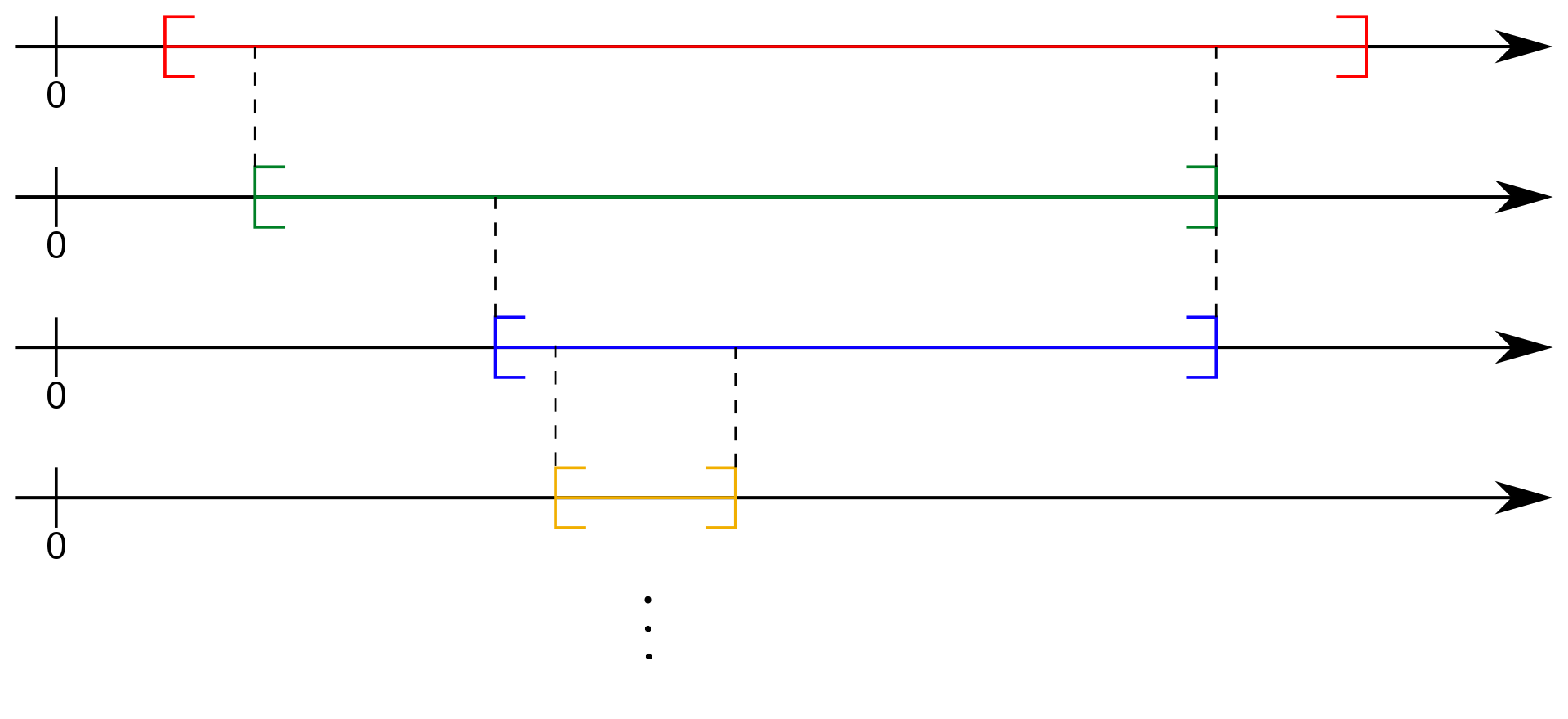
※ 축소구간열의 임의의 한 구간은 앞선 구간에 모두 포함되므로, 축소구간성질의 마지막 결론은 임의의 자연수 $n\in \mathbb{N}$ 에 대하여 $I_n$ 이 원소를 적어도 하나 가진다고 하여도 된다.

 

proof)

  $\bigcap _{n=1}^{\mathrm{\infty }}{I}_n$ 가 공집합이 아님을 보이기 위해서는 모든 $n\in \mathbb{N}$ 에 대하여 $x\in I_n$ 을 만족하는 실수 $x$ 가 존재함을 보이면 된다. 다음과 같은 집합 $A$ 를 생각하자.

$$A=\{a_n:n\in \mathbb{N}\}$$

  집합 $A$ 는 닫힌 구간열의 왼쪽 끝점으로 이루어진 집합이다. 이때 왼쪽 끝점들은 임의의 오른쪽 끝점 $b_n$ 보다 클 수 없으므로, 모든 $b_n$ 은 $A$ 의 상계이며 $A$ 는 위로 유계이다. 그러므로 완비성 공리에 따라 $A$ 의 상한 $\alpha =\text{sup}A$ 가 존재한다. 임의의 자연수 $n$ 을 고정하자. $\alpha$ 는 $A$ 의 상계이므로 $a_n\le \alpha$ 이며, 각각의 $b_n$ 이 $A$ 의 상계라는 점에서 $\alpha \le b_n$ 임을 알 수 있다.

  정리하면 모든 자연수 $n$ 에 대하여 $a_n\le \alpha \le b_n$ , 즉 $\alpha \in I_n$ 이다. 따라서 $\alpha \in \bigcap _{n=1}^{\mathrm{\infty }}{I}_n$ 이므로 원하는 결과를 얻는다.   $◻$

 

 

  축소구간성질의 아이디어로 실수의 소수전개를 계산하는 방법은 링크 참조.

 

 

2.2. 제곱근의 존재성

 

  지난 포스트에서 유리수로는 제곱해서 2가 되는 길이에 대응하는 수가 존재하지 않는 것을 확인하였다. 다음의 정리를 확인하며 실수를 발명한 보람을 느껴보자.

 

정리 2.2-1)  ${\alpha }^2=2$ 를 만족하는 실수 $\alpha \in \mathbb{R}$ 가 존재한다.

 

proof)

  다음과 같이 집합 $A$ 를 생각하자.

$$A=\{x\in \mathbb{R}:x^2<2\}$$

  완비성 공리에 따라 $A$ 의 최소상계 $\alpha =\text{sup}A$ 가 존재한다. $\mathbb{R}$ 은 순서체이므로 ${\alpha }^2<2$ , ${\alpha }^2=2$ , ${\alpha }^2>2$ 셋중에 하나만 성립한다. ${\alpha }^2=2$ 를 제외한 나머지는 불가능하다는 것을 보이는 것이 본 증명의 전략이다.

  ${\alpha }^2<2$ 라고 가정하자. 이때 $\alpha$ 보다 큰 $A$ 의 원소를 찾아 모순을 보이자. 임의의 자연수 $n$ 에 대하여 다음이 성립한다.

$$\begin{array}{rl}{(\alpha +\frac{1}{n})}^2& ={\alpha }^2+\frac{2\alpha }{n}+\frac{1}{n^2}\\ & \le {\alpha }^2+\frac{2\alpha }{n}+\frac{1}{n}={\alpha }^2+\frac{2\alpha +1}{n}\end{array}$$

  아르키메데스 성질에 따라 다음을 만족하는 자연수 $n_0$ 이 존재한다.

$$2\alpha +1<n_0(2-{\alpha }^2)$$

  이 자연수 $n_0$ 에 대하여 다음이 성립한다.

$${(\alpha +\frac{1}{n_0})}^2\le {\alpha }^2+\frac{2\alpha +1}{n_0}<{\alpha }^2+(2-{\alpha }^2)=2$$

  따라서 $\alpha +\frac{1}{n_0}$ 은 $A$ 의 원소이며, 이는 $\alpha$ 가 $A$ 의 상계라는 사실에 모순된다. 그러므로 ${\alpha }^2<2$ 가 아니다.

  ${\alpha }^2>2$ 라고 가정하자. 이때 $\alpha$ 보다 작은 $A$ 의 상계를 찾아 모순을 보이자. 임의의 자연수 $n$ 에 대하여 다음이 성립한다.

$${(\alpha -\frac{1}{n})}^2={\alpha }^2-\frac{2\alpha }{n}+\frac{1}{n^2}>{\alpha }^2-\frac{2\alpha }{n}$$

  아르키메데스 성질에 따라 다음을 만족하는 자연수 $n_0$ 이 존재한다.

$$2\alpha <n_0({\alpha }^2-2)$$

  이 자연수 $n_0$ 에 대하여 다음이 성립한다.

$${(\alpha -\frac{1}{n_0})}^2>{\alpha }^2-\frac{2\alpha }{n_0}>{\alpha }^2-({\alpha }^2-2)=2$$

  따라서 $\alpha -\frac{1}{n_0}$ 는 $A$ 의 상계이며, 이는 $\alpha$ 가 $A$ 의 최소상계라는 사실에 모순된다. 그러므로 ${\alpha }^2>2$ 가 아니다.

  ${\alpha }^2<2$ 와 ${\alpha }^2>2$ 가 거짓이므로, 순서체의 성질에 따라 ${\alpha }^2=2$ 가 성립한다.   $◻$

 

 

  위의 정리를 일반화하면 다음의 결론을 얻을 수 있다. 그 증명 과정은 거의 비슷하다.

 

정리 2.2-2)  임의의 $x\ge 0$ 와 자연수 $m\in \mathbb{N}$ 에 대하여 ${\alpha }^m=x$ 를 만족하는 실수 $\alpha \in \mathbb{R}$ 가 존재한다.

 

proof)

  다음과 같이 집합 $A$ 를 생각하자.

$$A=\{t\in \mathbb{R}:t^m<x\}$$

  완비성 공리에 따라 $A$ 의 최소상계 $\alpha =\text{sup}A$ 가 존재한다. $\mathbb{R}$ 은 순서체이므로 ${\alpha }^m<x$ , ${\alpha }^m=x$ , ${\alpha }^m>x$ 셋중에 하나만 성립한다.

  ${\alpha }^m<x$ 라고 가정하자. 이때 $\alpha$ 보다 큰 $A$ 의 원소를 찾아 모순을 보이자. 임의의 자연수 $n$ 에 대하여 이항정리를 사용하면 다음과 같다.

$$\begin{array}{rl}& {(\alpha +\frac{1}{n})}^m\\ & =\sum _{k=1}^m(\genfrac{}{}{0ex}{}{m}{k})\frac{{\alpha }^{m-k}}{n^k}\\ & ={\alpha }^m+(\genfrac{}{}{0ex}{}{m}{1})\frac{{\alpha }^{m-1}}{n}+(\genfrac{}{}{0ex}{}{m}{2})\frac{{\alpha }^{m-2}}{n^2}+\cdots +\frac{1}{n^m}\\ & \le {\alpha }^m+\frac{1}{n}\{(\genfrac{}{}{0ex}{}{m}{1}){\alpha }^{m-1}+(\genfrac{}{}{0ex}{}{m}{2}){\alpha }^{m-2}+\cdots +1\}\end{array}$$

  아르키메데스 성질에 따라 다음을 만족하는 자연수 $n_0$ 이 존재한다.

$$(\genfrac{}{}{0ex}{}{m}{1}){\alpha }^{m-1}+(\genfrac{}{}{0ex}{}{m}{2}){\alpha }^{m-2}+\cdots +1<n_0(x-{\alpha }^m)$$

  이 자연수 $n_0$ 에 대하여 다음이 성립한다.

$$\begin{array}{rl}& {(\alpha +\frac{1}{n_0})}^m\\ & \le {\alpha }^m+\frac{1}{n_0}\{(\genfrac{}{}{0ex}{}{m}{1}){\alpha }^{m-1}+(\genfrac{}{}{0ex}{}{m}{2}){\alpha }^{m-2}+\cdots +1\}\\ & <{\alpha }^m+(x-{\alpha }^m)=x\end{array}$$

  따라서 $\alpha +\frac{1}{n_0}$ 은 $A$ 의 원소이며, 이는 $\alpha$ 가 $A$ 의 상계라는 사실에 모순된다. 그러므로 ${\alpha }^m<x$ 가 아니다.

  ${\alpha }^m>x$ 라고 가정하자. 이때 $\alpha$ 보다 작은 $A$ 의 상계를 찾아 모순을 보이자. 임의의 자연수 $n$ 에 대하여 이항정리를 사용하면 다음과 같다.

$$\begin{array}{rl}& {(\alpha -\frac{1}{n})}^m\\ & =\sum _{k=0}^m(\genfrac{}{}{0ex}{}{m}{k}){\alpha }^{m-k}{(-\frac{1}{n})}^k\\ & ={\alpha }^m-(\genfrac{}{}{0ex}{}{m}{1})\frac{{\alpha }^{m-1}}{n}+(\genfrac{}{}{0ex}{}{m}{2})\frac{{\alpha }^{m-2}}{n^2}-\cdots +\frac{(-1{)}^m}{n^m}\end{array}$$

  $m$ 보다 작은 최대 홀수를 $m^{\ast }$ 라고 하자. 위의 식에서 ${\alpha }^m$ 을 제외한 양수항을 모두 제거하면 다음이 성립한다.

$$\begin{array}{rl}& {\alpha }^m-(\genfrac{}{}{0ex}{}{m}{1})\frac{{\alpha }^{m-1}}{n}+(\genfrac{}{}{0ex}{}{m}{2})\frac{{\alpha }^{m-2}}{n^2}-\cdots +\frac{(-1{)}^m}{n^m}\\ & >{\alpha }^m-(\genfrac{}{}{0ex}{}{m}{1})\frac{{\alpha }^{m-1}}{n}-(\genfrac{}{}{0ex}{}{m}{3})\frac{{\alpha }^{m-3}}{n^3}-\cdots -(\genfrac{}{}{0ex}{}{m}{m^{\ast }})\frac{{\alpha }^{m-m^{\ast }}}{n^{m^{\ast }}}\\ & \ge {\alpha }^m-\frac{1}{n}\{(\genfrac{}{}{0ex}{}{m}{1}){\alpha }^{m-1}+(\genfrac{}{}{0ex}{}{m}{3}){\alpha }^{m-3}+\cdots +(\genfrac{}{}{0ex}{}{m}{m^{\ast }}){\alpha }^{m-m^{\ast }}\}\end{array}$$

  아르키메데스 성질에 따라 다음을 만족하는 자연수 $n_0$ 이 존재한다.

$$(\genfrac{}{}{0ex}{}{m}{1}){\alpha }^{m-1}+(\genfrac{}{}{0ex}{}{m}{3}){\alpha }^{m-3}+\cdots +(\genfrac{}{}{0ex}{}{m}{m^{\ast }}){\alpha }^{m-m^{\ast }}<n_0({\alpha }^m-x)$$

  이 자연수 $n_0$ 에 대하여 다음이 성립한다.

$$\begin{array}{rl}& {(\alpha -\frac{1}{n_0})}^m\\ & >{\alpha }^m-\frac{1}{n_0}\{(\genfrac{}{}{0ex}{}{m}{1}){\alpha }^{m-1}+(\genfrac{}{}{0ex}{}{m}{3}){\alpha }^{m-3}+\cdots +(\genfrac{}{}{0ex}{}{m}{m^{\ast }}){\alpha }^{m-m^{\ast }}\}\\ & >{\alpha }^m-({\alpha }^m-x)=x\end{array}$$

  따라서 $\alpha -\frac{1}{n_0}$ 는 $A$ 의 상계이며, 이는 $\alpha$ 가 $A$ 의 최소상계라는 사실에 모순된다. 그러므로 ${\alpha }^m>x$ 가 아니다.

  ${\alpha }^m<x$ 와 ${\alpha }^m>x$ 가 거짓이므로, 순서체의 성질에 따라 ${\alpha }^m=x$ 가 성립한다.   $◻$

 

 

  위의 정리에서 존재성을 밝힌 $\alpha$ 는 $\sqrt[m]{x}$ 라고 쓴다.

 

 

읽어주셔서 감사합니다.

 

  이전 읽을거리 : [FTC의 엄밀한 증명] ch1. 실수의 정의

  다음 읽을거리 :

  [FTC의 엄밀한 증명] ch3. 수열의 극한

  [직선과 실수] ch1. 순서체의 엄밀한 정의