[선형변환부터 동형사상까지] ch8. 동형사상

  이전 읽을거리 : [선형변환부터 동형사상까지] ch7. 가역인 선형변환

 

  본 포스팅은 '프리드버그 선형대수학(5판)'을 공부하며 작성하였습니다.

 

 

11. 동형사상

 

※ 본 포스팅의 도입부는 다소 엄밀하지 못하므로, 대수구조 및 동형에 대해 자세하게 공부하실 분은 'Fraleigh. A first course in abstract algebra' 또는 타 블로그 생새우초밥집을 참고하시길 바랍니다.

 

  체스를 두자. 여러가지 선택지가 있을 수 있다. 상아로 된 말을 쑬 수도 있고, 나무로 된 말을 쓸 수도 있다. 아니면 운동장에 나가서 바닥에 줄을 긋고 친구들을 세워 체스를 할 수도 있다. 모두 다 다른 형식을 갖추었지만, 중요한건 체스의 룰은 그대로라는 것이다. 우리가 체스라고 부르는 것은 분명히 규칙 그 자체를 지칭한다.

 

  수학에서도 우리가 사과를 더하든, 원숭이를 더하든, 추상화된 수학적 대상인 자연수를 더하든, 총 갯수를 헤아리려는 목적 속의 덧셈이라는 연산 규칙은 변함이 없다. 좀더 나아가보자.

 

  사과 한 개의 묶음(?)을 1에 대응하고, 사과 두 개의 묶음을 2에 대응하고, 사과 세 개의 묶음을 3에 대응하고... 이러한 일대일대응을 구태여 함수 $\phi$ 로 나타내보자. 사과 묶음 집합으로부터 자연수 집합으로 가는 함수 $\phi$ 는 구체적으로 다음과 같다. (이 함수가 전단사임은 자명하다)

$$\phi(\mbox{one apple})=1$$

$$\phi(\mbox{two apples})=2$$

$$\phi(\mbox{three apples})=3$$

$$\vdots$$

  두 묶음을 풀어 한 묶음으로 만드는 과정을 생각해보자. 사과 두 개의 묶음과 사과 세 개의 묶음을 각각 풀어 한 묶음으로 만들면 사과 다섯 개의 묶음이 될 것이다. 이를 다음과 같이 써보자.

$$\mbox{two apples}\odot\mbox{three apples}=\mbox{five apples}\tag{1}$$

  연산 기호 $\odot$ 는 양쪽의 두 묶음을 하나의 묶음으로 만든다는 의미로 사용해보았다. 그리고 다음은 너무나도 자명하다.

$$2+3=5\tag{2}$$

  식 (1)과 식 (2)는 연산의 구체적인 설명 및 원소를 가져온 집합만 다르며, 우리 마음속으론 똑같은 짓을 반복한다고 생각하고 있을 것이다. 대응 $\phi$ 로 식 (2)를 다시 나타내면 다음과 같다.

$$\begin{align}&\phi(\mbox{two apples})+\phi(\mbox{three apples})\\=&\phi(\mbox{five apples})\\=&\phi(\mbox{two apples}\odot\mbox{three apples})\end{align}$$

  무언가 규칙같은것이 만들어졌다. 이 과정을 무수히 반복한다면, 사과 묶음 집합의 임의의 두 원소 $A,\;B$ 에 대하여 다음의 식이 항상 성립한다는 것을 알 수 있을 것이다. 사실 우리는 충분히 알고있다.

$$\phi(A\odot B)=\phi(A)+\phi(B)$$

  위의 식은 두 연산 규칙이 사실은 동일하다는 증거이다. 사과 묶음 집합의 원소 $A,\;B$ , $C=A\odot B$ 에 각각 대응하는 자연수 $a,\;b$ , $c=a+b$ 에 대하여 그림으로 표현하면 다음과 같다.

 

출발과 도착이 같다면 경로에 관계없이 같다.

 

  위 다이어그램을 보면, 이쪽에서 연산하는 것과 저쪽에서 연산하는 것은 그 연산 구조가 동일하다는 것을 느낄 수 있다. $\phi$ 는 사과묶음을 자연수로, $\odot$ 을 $+$ 로 교환하는 이름바꾸기에 불구하다.

 

  다음의 정의로써, 우리는 둘 사이에 이름바꾸기가 존재하는 것들을 '같은 것'으로 볼 것이다.

 

보조정의)  연산 $*$ 가 정의된 집합 $S$ , 연산 $*'$ 가 정의된 집합 $S'$ 를 생각하자. 임의의 원소 $x,\;y\in S$ 에 대하여 다음을 만족하는 전단사함수 $\phi:S\to S'$ 가 존재하면 $S$ 는 $S'$ 와 동형이라 하며 $S\simeq S'$ 라고 쓴다.$$\phi(x*y)=\phi(x)*'\phi(y)$$  이때 $\phi$ 는 동형사상이라 한다.

 

  그러나 이 정의는 벡터공간의 특징 중 하나인 스칼라 곱을 보존하는 동형사상에 대해서는 설명하지 못한다. 벡터공간은 합 이외에도 체와 벡터를 곱하는 특이한 연산인 스칼라 곱까지 정의된다. 따라서 두 벡터공간 사이의 동형사상은 두 연산 모두 보존해야 한다. 자연스럽게 다음과 같이 다시 정의하자.

 

정의)  합 '$+$' 과 스칼라 곱 '$\cdot$' 이 정의된 $F$-벡터공간 $V$ , 합 '$\textcolor{red}{+}$' 과 스칼라 곱 '$\textcolor{red}{\cdot}$' 이 정의된 $F$-벡터공간 $W$ 를 생각하자. 임의의 벡터 $x,\;y\in V$ 및 스칼라 $c\in F$ 대하여 다음을 만족하는 전단사함수 $\phi:V\to W$ 가 존재하면 $V$ 는 $W$ 와 동형(Isomorphic)이라 하며 $V\simeq W$ 라고 쓴다.$$\phi(x+y)=\phi(x)\textcolor{red}{+}\phi(y)$$$$\phi(c\cdot x)=c\textcolor{red}{\cdot}\phi(x)$$  이때 $\phi$ 는 동형사상(Isomorphism)이라 한다.

 

  스칼라 곱에 대한 조건이 왜 이렇게 추가되었는지는 아래의 다이어그램을 유심히 살펴보면 알 수 있다.

 

직접 그린 다이어그램. 마찬가지로 출발과 도착이 같다면 경로에 관계없이 같다.

 

  두 벡터공간 사이에 동형사상이 존재한다면, 두 벡터공간의 합과 스칼라 곱을 각각 '같은 것'으로 보자는 것이다. 두 벡터공간이 동형이라면 이름바꾸기^[각주:1]에 지나지 않기 때문이다. 단, 두 벡터공간 속 벡터의 '모양'은 서로 다를 수 있다. 하지만 벡터는 연산하기 위해 사용하는 것이므로 연산의 맥락에서 같은 것으로 보는 것이다.

 

 

11.1. 동형사상의 성질

 

  벡터공간에서 동형이 정의되는 것을 보고있자면 다음의 정리가 생각이 나지 않을 수 없다.

 

정리 11.1-1)  두 벡터공간 $V,\;W$ 에 대하여 $V\simeq W$ 이기 위한 필요충분조건은 가역인 선형변환 $T:V\to W$ 가 존재하는 것이며, 이때 $T$ 는 동형사상이다.

 

proof)

  $V$ 는 $W$ 와 동형일 때를 생각하자. $V$ 에서 $W$ 로 가는 동형사상 $\phi$ 가 존재하며, 동형사상의 정의에 따라 $\phi$ 는 전단사이며 선형이다. 정리 0.4.1-1에 따르면 $\phi$ 는 가역이므로 $V$ 에서 $W$ 로 가는 가역인 선형변환이다.

 

  가역인 선형변환 $T:V\to W$ 가 존재할 때를 생각하자. 정리 0.4.1-1에 따라 $T$ 는 전단사이며 선형변환의 정의에 따라 동형사상의 조건을 모두 만족한다. 즉 $T$ 는 동형사상이다.   $\square$

 

 

  다음의 정리에 따르면 동형은 동치관계이다. 즉, $V$ 는 $W$ 와 동형이라고 하든 $W$ 는 $V$ 와 동형이라고 하든 상관 없다. 그저 $V$ 와 $W$ 는 동형인 것이다.

 

정리 11.1-2)  세 $F$-벡터공간 $V,\;W,\;Z$ 에 대하여 다음의 세 명제가 성립한다.
  (ⅰ) $V\simeq V$
  (ⅱ) $V\simeq W\iff W\simeq V$
  (ⅲ) $V\simeq W\;\mbox{ And }\;W\simeq Z\implies V\simeq Z$

 

proof)

  (ⅰ) : $V$ 에서 정의된 항등변환 $I_V$ 를 생각하자. $I_V$ 는 항등함수이므로 정리 0.2-1에 따라 전단사이며 정리 0.4.1-1에 따라 가역이다. 정리 11.1-1에 따라 $V$ 는 $V$ 와 동형이다.

 

  (ⅱ) : $V$ 는 $W$ 와 동형일 경우 가역인 선형변환 $T:V\to W$ 가 존재한다. $T^{-1}:W\to V$ 는 정리 0.4.1-4에 따라 가역이므로 정리 11.1-1에 따라 $W$ 는 $V$ 와 동형이다.

 

  (ⅲ) : $V$ 는 $W$ 와 동형일 경우 가역인 선형변환 $T:V\to W$ 가 존재하며, $W$ 는 $Z$ 와 동형일 경우 가역인 선형변환 $U:W\to Z$ 가 존재한다. $T$ 와 $U$ 는 가역이며 전단사이고, 정리 0.3.1-1(ⅲ)에 따라 $UT:V\to Z$ 는 전단사이므로 가역이다. $V$ 에서 $Z$ 로 가는 동형사상이 존재하므로 $V$ 는 $Z$ 와 동형이다.   $\square$

 

 

  그래서 결국 어떤 벡터공간과 어떤 벡터공간이 동형이라는 것인가? 이 질문은 다음 정리로 완벽하게 해소된다.

 

정리 11.1-3)  유한차원 $F$-벡터공간 $V,\;W$ 에 대하여 $V\simeq W$ 이기 위한 필요충분조건은 $\mbox{dim}(V)=\mbox{dim}(W)$ 인 것이다.

 

proof)

  $V$ 와 $W$ 가 동형일 때를 생각하자. 동형사상 $T:V\to W$ 가 존재하며, 정리 10-3에 따라 $\mbox{dim}(V)=\mbox{dim}(W)$ 가 성립한다.

 

  $\mbox{dim}(V)=\mbox{dim}(W)$ 일 때를 생각하자. $V,\;W$ 각각의 순서기저를 $\beta,\;\gamma$ 라고 하자. $\beta,\;\gamma$ 를 이루는 벡터의 갯수가 서로 같으므로 $n=\mbox{dim}(V)$ 이라고 하면 선형변환의 존재성 및 유일성 정리 2에 따라 $I_n=[T]_\beta^\gamma$ 를 만족하는 선형변환 $T:V\to W$ 가 존재한다. $I_nI_n=I_n$ 이므로 $I_n$ 은 가역이며 정리 10.2-1에 따라 $T$ 는 가역이다. 정리 11.1-1에 따라 $T$ 는 $V$ 에서 $W$ 로 가는 동형사상이므로 $V$ 와 $W$ 는 동형이다.   $\square$

 

 

  이제는 말할 수 있다. n-순서쌍의 집합인 $F^n$ 과 성분이 n개인 열벡터의 집합 $\mathbb{M}_{n\times 1}(F)$ 를 동일하게 취급한 것은 두 벡터공간이 동형이기 때문이었다. 고등학교 수학교육과정에서 (유클리드) 3차원 공간의 유향선분(화살표)과 3-순서쌍을 같은 것이라 취급했던 것도 마찬가지다.

 

  다음의 자명한 정리는 모든 n차원 $F$-벡터공간이 $F^n$ 과 동형이라고 말하고 있다.

 

정리 11.1-4)  $F$-벡터공간 $V$ 에 대하여 $V\simeq F^n$ 이기 위한 필요충분조건은 $\mbox{dim}(V)=n$ 인 것이다.

 

  심지어 $\mathcal{L}(V,W)$ 와 $\mathbb{M}_{m\times n}(F)$ 도 동형이다. 이는 정말 문장 그대로 '선형변환과 행렬은 같은 것'이라는 말이다. 혹시 '선형변환을 행렬표현에 대응시키는 사상'을 함수로 다룰 것이라 예고한 것을 기억하는가? 그때가 바로 지금이다.

 

선형대수학의 기본정리^[각주:2])  차원이 각각 n, m 인 $F$-벡터공간 $V,\;W$ 각각의 순서기저 $\beta,\;\gamma$ 를 생각하자. 다음과 같이 정의한 함수 $\Phi_\beta^\gamma$ 는 동형사상이다.$$\Phi_\beta^\gamma:\mathcal{L}(V,W)\to\mathbb{M}_{m\times n}(F),\;T\mapsto[T]_\beta^\gamma$$  즉, $\mathcal{L}(V,W)$ 와 $\mathbb{M}_{m\times n}$ 는 동형이다.

 

※ $\mathcal{L}(V,W)$ 이 무엇인지 기억이 나지 않는다면 5.1. 선형변환의 집합인 벡터공간 참고

 

proof)

  정리 5.2-1에 따라 $\Phi_\beta^\gamma$ 는 선형이며 선형변환의 존재성 및 유일성 정리 2와 정리 0.1.3-1을 종합하여 $\Phi_\beta^\gamma$ 는 전단사임을 알 수 있다. 즉 $\Phi_\beta^\gamma$ 는 가역인 선형변환이므로 $\mathcal{L}(V,W)$ 에서 $\mathbb{M}_{m\times n}(F)$ 로 가는 동형사상이다.   $\square$

 

  다음의 따름정리는 꽤나 신기한 사실을 알려준다. $\mathcal{L}(V,W)$ 의 차원을 궁금해하는 사람이 있을진 모르겠지만..

 

선형대수학의 기본정리의 따름정리)  차원이 각각 n, m인 벡터공간 $V,\;W$ 에 대하여 $\mathcal{L}(V,W)$ 의 차원은 mn이다.

 

proof)

  7.1. 기저의 예시에서 보다시피 $\mathbb{M}_{m\times n}(F)$ 의 기저를 이루는 벡터의 수는 mn개이다. 즉 $\mathbb{M}_{m\times n}(F)$ 의 차원은 mn이며, 정리 11.1-5에 따라 $\mathbb{M}_{m\times n}(F)\simeq\mathcal{L}(V,W)$ 이므로 정리 11.1-3에 따라 $\mathcal{L}(V,W)$ 의 차원도 mn이다.   $\square$

 

 

11.2. 선형대수의 목적

 

※ 시리즈를 마치며 신나는 마음에 제목은 좀 과장하였습니다..

 

  선형대수학의 어머니는 행렬이다. 행렬표현부터 동형사상에 이르기까지 수많은 노력들은 모든 선형변환을 행렬로 환원시키려는 시도였다. 그리고 지금에 이르러 노력의 결실을 맺을 수 있게 되었다.

 

  본 시리즈의 마지막 정의를 하자. 이것도 마찬가지로 예고된 바 있는 정의이다.

 

정의)  n차원 $F$-벡터공간 $V$ 의 순서기저를 $\beta$ 라 하자. $\beta$ 에 대한 $V$ 의 표준표현(standard representation)은 다음과 같이 정의된 함수 $\phi$ 이다.$$\phi:V\to F^n,\;x\mapsto[x]_\beta$$

 

  이 함수가 무엇을 뜻하는지는 좌표벡터를 공부하였으면 바로 알 것이다.

 

  다음의 정리는 n차원 벡터공간에서 $F^n$ 으로 가는 구체적인 동형사상을 제안한다.

 

정리 11.2-1)  임의의 n차원 $F$-벡터공간 $V$ 와 순서기저 $\beta$ 를 생각하자. $\phi_\beta$ 는 $V$ 에서 $F^n$ 으로 가는 동형사상이다.

 

proof)

  정리 4.1-1에 따라 $\phi_\beta$ 는 선형이며 보조정리 5.2-3와 정리 0.1.3-1를 종합하면 $\phi_\beta$ 는 전단사임을 알 수 있다. 즉 $\phi_\beta$ 는 가역인 선형변환이므로 $V$ 에서 $F^n$ 로 가는 동형사상이다.   $\square$

 

  각각 n, m차원인 두 벡터공간 $V,\;W$ 각각의 순서기저 $\beta,\;\gamma$ 를 생각하자. $V\simeq F^n$ 이며, $W\simeq F^m$ 이다. 정리 11.2-1에 따라 $V$ 에서 $F^n$ 로 가는 동형사상 $\phi_\beta$ , $W$ 에서 $ F^m$ 로 가는 동형사상 $\phi_\gamma$ 가 있다.

 

  $V$ 에서 $W$ 로 가는 임의의 선형변환 $T$ 를 생각해보자. $L_{[T]_\beta^\gamma}$ 는 $ F^n$ 에서 $F^m$ 로 가는 선형변환이다. 다음의 그림을 그려볼 수 있다.

 

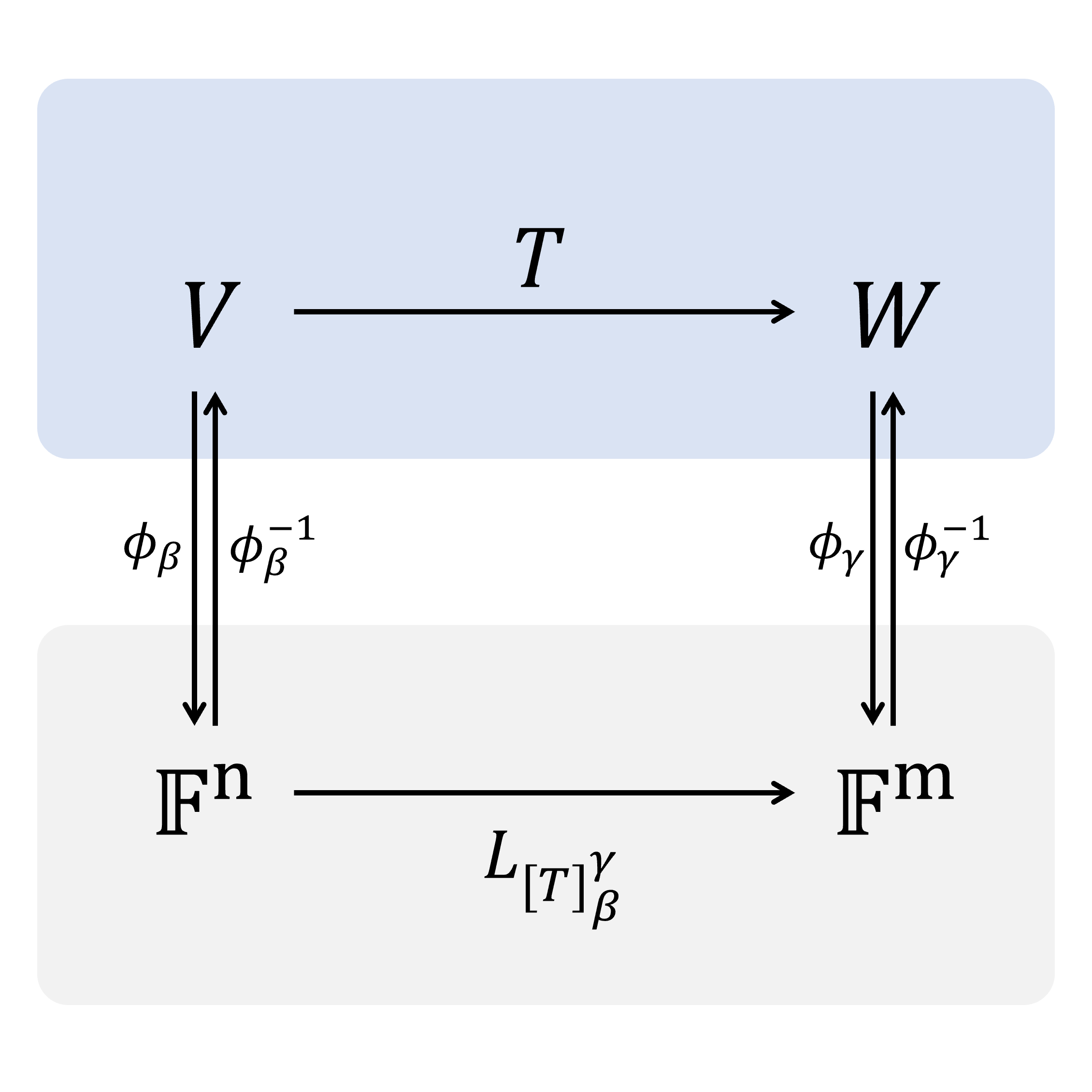
  다음의 정리에 따르면 위 다이어그램은 도착과 출발이 같다면 모든 합성함수는 경로에 무관하게 같은 함수이다. 즉 위 다이어그램은 가환적(commutative)이다. 동형을 소개할 때 보인 다이어그램과 비교해보면 $T$ 와 $L_{[T]_\beta^\gamma}$ 의 연산 구조가 동일하다는것을 다시 느낄 수 있다.

 

정리 11.2-2)  각각 n, m차원인 벡터공간 $V,\;W$ 의 순서기저 $\beta,\;\gamma$ 를 생각하자. 임의의 선형변환 $T:V\to W$ 에 대하여 다음이 성립한다.$$\begin{align}L_{[T]_\beta^\gamma}\phi_\beta=&\phi_\gamma T\\T\phi_\beta^{-1}=&\phi_\gamma^{-1}L_{[T]_\beta^\gamma}\\T=&\phi_\gamma^{-1}L_{[T]_\beta^\gamma}\phi_\beta\\L_{[T]_\beta^\gamma}=&\phi_\gamma T\phi_\beta^{-1}\end{align}$$

 

proof)

  임의의 벡터 $x\in V$ 에 대하여 다음이 성립한다.

$$L_{[T]_\beta^\gamma}\phi_\beta(x)=L_{[T]_\beta^\gamma}([x]_\beta)=[T]_\beta^\gamma[x]_\beta$$

$$\phi_\gamma T(x)=[T(x)]_\gamma$$

  정리 8-1에 따르면 $[T(x)]_\gamma=[T]_\beta^\gamma[x]_\beta$ 이므로 $L_{[T]_\beta^\gamma}\phi_\beta=\phi_\gamma T$ 가 성립한다. 이 결과로부터 나머지는 자명하게 성립한다.   $\square$

 

  위 정리에서 가장 중요한 식은 $T=\phi_\gamma^{-1}L_{[T]_\beta^\gamma}\phi_\beta$ 이다. 이는 모든 선형변환이 열벡터를 행렬에 곱하는 것으로 대체될 수 있다는 사실을 말한다. 여기서 동형사상은 단지 이름바꾸기에 지나지 않음을 기억하자.

 

---

  예로, 선형변환 $T:\mathbb{P}_3(\mathbb{R})\to\mathbb{P}_2(\mathbb{R}),\;f(x)\mapsto f'(x)$ 를 생각하자. $\mathbb{P}_3(\mathbb{R}),\;\mathbb{P}_2(\mathbb{R})$ 각각의 표준 순서기저 $\beta,\;\gamma$ 에 대하여 $T$ 의 행렬표현이 다음과 같음은 쉽게 구할 수 있다.

$$[T]_\beta^\gamma=\begin{pmatrix}0&1&0&0\\0&0&2&0\\0&0&0&3\end{pmatrix}$$

  아무 다항식이나 $T$ 에 대입해보자. $p(x)=1-3x+5x^2-7x^3$ 에 대하여 $T(p(x))$ 는 다음과 같다.

$$T(p(x))=p'(x)=-3+10x-21x^2$$

  한편 $\phi_\gamma^{-1}L_{[T]_\beta^\gamma}\phi_\beta(p(x))$ 를 계산해보면 다음과 같다.

$$\phi_\beta(p(x))=\begin{pmatrix}1\\-3\\5\\-7\end{pmatrix}$$

$$\begin{align}L_{[T]_\beta^\gamma}\phi_\beta(p(x))=&\begin{pmatrix}0&1&0&0\\0&0&2&0\\0&0&0&3\end{pmatrix}\begin{pmatrix}1\\-3\\5\\-7\end{pmatrix}\\=&\begin{pmatrix}-3\\10\\-21\end{pmatrix}\end{align}$$

$$\therefore\phi_\gamma^{-1}L_{[T]_\beta^\gamma}\phi_\beta(p(x))=-3+10x-21x^2$$

  따라서 $T=\phi_\gamma^{-1}L_{[T]_\beta^\gamma}\phi_\beta$ 가 성립한다는 사실로부터 선형변환이 행렬연산으로 대체됨을 확인하였다.

---

 

 

글 작성에 상당히 공을 많이 들였습니다.. 지금까지 본 시리즈를 찾아주신 모든 분들께 감사드립니다.

1. 마치 '사과 묶음 합치기'와 '덧셈'을 같은 행위로 보듯이 [본문으로]
2. 미적분학의 기본정리, 대수학의 기본정리 등 유명한 기본정리들과는 달리 본 정리에 '기본정리'라는 명칭이 붙는 것은 일반적이지 않다. 본 정리에 이러한 이름을 붙이는 것은 '이인석. 선형대수와 군'에 따랐다. [본문으로]