[변수변환정리] ch1. 단위분할

이전 읽을거리)

[다변수 미분] ch1. 미분의 정의

[다변수 적분] ch1. 적분의 정의

다음 읽을거리: ch2. 미분동형사상

---

  Convention.
  ▷ ${\mathcal{T}}_{{\mathbb{R}}^n}$ 이란 ${\mathbb{R}}^n$ 에서 열린집합의 모임이다.
  ▷ ${\mathcal{N}}_{{\mathbb{R}}^n}(x)$ 란 $x\in {\mathbb{R}}^n$ 의 근방의 모임, 즉 ${\mathbb{R}}^n$ 에서 열린 $x$ 를 포함하는 집합의 모임이다.
  ▷ $\mathcal{Q}({\mathbb{R}}^n)$ 이란 ${\mathbb{R}}^n$ 의 rectangles 의 모임이다. (비표준)

 

 

 

몇 가지 도움정리

 

 

  이번 포스팅에서 알아볼 개념은 단위분할로, 조그만 부분을 다 더해서 전체로 확장시키는 개념을 갖는 도구이다. 자세한 정의를 확인하면 무엇을 의미하는지 확실하게 드러나지만, 그 존재성의 증명은 쉽지만은 않다. 다음의 도움정리부터 시작하자.

 

 

  Lemma 1.1 (베르누이 부등식, Bernoulli's inequality).
  임의의 $x\in (-1,\mathrm{\infty })$ 와 임의의 $n\in \mathbb{N}$ 에 대해 다음 부등식이 성립한다.$$(1+x{)}^n\ge 1+nx$$

 

 

  Proof.  $n$ 에 대한 귀납법으로 증명하자. $n=1$ 인 경우 정리가 자명하게 성립한다. $n-1$ 에서 정리가 성립한다고 가정하고 $n$ 에서 정리가 성립함을 보이자. 다음 식이 성립하므로 원하는 결과를 얻는다.

$$\begin{array}{rl}(1+x{)}^n& =(1+x)(1+x{)}^{n-1}\\ & \ge (1+x)(1+(n-1)x)\\ & =1+nx+(n-1)x^2\\ ◻& & \ge 1+nx\end{array}$$

 

 

 

Lemma 1.2.  다음의 함수 $f:\mathbb{R}\to \mathbb{R}$ 은 $C^{\mathrm{\infty }}$ 급이다.$$f(x)=\{\begin{array}{ll}{e}^{-\frac{1}{x}}& \text{if }x>0\\ 0& \text{otherwise}\end{array}$$

 

 

  Proof.  각 $n\in \mathbb{N}$ 에 대해 다음의 함수 $f_n:\mathbb{R}\to \mathbb{R}$ 을 정의하자.

$$f_n(x)=\{\begin{array}{ll}\frac{e^{-\frac{1}{x}}}{x^n}& \text{if }x>0\\ 0& \text{otherwise}\end{array}$$

 

  Step 1. 임의의 $x\in \mathbb{R}$ 에 대해 $e^x>x$ 임을 보이자. $x<0$ 인 경우에는 $e^x>0$ 이므로 자명하게 성립한다. $x\ge 0$ 이라고 가정하자. 임의의 $n\in \mathbb{N}$ 에 대해 베르누이 부등식에 따라 다음이 성립한다.

$${(1+\frac{x}{n})}^n\ge 1+x$$

  따라서 다음이 성립하므로 원하는 결과를 얻는다.

$$e^x=\underset{n\to \mathrm{\infty }}{lim}{(1+\frac{x}{n})}^n\ge 1+x>x$$

 

  Step 2. $f$ 가 연속임을 보이자. 이는 $0$ 에서 연속임을 보이는 것 만으로도 충분하다. 임의의 $ϵ>0$ 에 대해 $\delta =ϵ$ 이라고 하자. $x\in (-\delta ,0]$ 인 경우 $|f(x)|=0$ 이므로 $|f(x)|<ϵ$ 이 자명하게 성립한다. $x\in (0,\delta )$ 인 경우 step 1 에 따라 다음이 성립한다.

$$e^{-\frac{1}{x}}=\frac{1}{e^{\frac{1}{x}}}<\frac{1}{\frac{1}{x}}=x$$

$$\therefore |f(x)|=|e^{-\frac{1}{x}}|=e^{-\frac{1}{x}}<x<ϵ$$

  정리하면 다음과 같으므로 원하는 결과를 얻는다.

$$|x|<\delta \Rightarrow |f(x)|<ϵ$$

 

  Step 3. $f_n$ 이 연속임을 보이자. 이는 $0$ 에서 연속임을 보이는 것 만으로도 충분하다. Step 1 에 따라 $x>0$ 에 대해 다음이 성립한다.

$$\begin{array}{rl}\frac{1}{2nx}<e^{\frac{1}{2nx}}& \iff \frac{1}{(2nx{)}^n}<e^{\frac{1}{2x}}\\ & \iff \frac{e^{-\frac{1}{x}}}{x^n}<(2n{)}^n{e}^{-\frac{1}{2x}}\end{array}$$

  따라서 임의의 $x\in \mathbb{R}$ 에 대해 다음이 성립한다.

$$0\le f_n(x)\le (2n{)}^{n}f(2x)$$

$$\therefore \frac{|f_n(x)|}{(2n{)}^n}\le |f(2x)|$$

  임의의 $ϵ>0$ 을 생각하자. Step 2 에 따라 $f(2x)$ 는 $0$ 에서 연속이므로 어떤 $\delta >0$ 이 존재하여 다음이 성립하므로 원하는 결과를 얻는다.

$$\begin{array}{rl}|x|<\delta & \Rightarrow |f(2x)|<\frac{ϵ}{(2n{)}^n}\\ & \Rightarrow |f_n(x)|<ϵ\end{array}$$

 

  Step 4. $f_n$ 이 미분가능함을 보이자. 이는 $0$ 에서 미분가능함을 보이는 것 만으로도 충분하다. $x\ne 0$ 에 대해 다음이 성립한다.

$$\frac{f_n(x)-f_n(0)}{x}=\frac{f_n(x)}{x}=f_{n+1}(x)$$

  한편 $f_{n+1}$ 은 step 3 에 따라 $0$ 에서 연속이므로 다음이 성립한다.

$$f_{n+1}(0)=\underset{x\to 0}{lim}{f}_{n+1}(x)=\underset{x\to 0}{lim}\frac{f_n(x)-f_n(0)}{x}$$

  따라서 $f_n$ 은 $0$ 에서 미분가능하며, 특히 $f_{n+1}(0)=0$ 이므로 $D{f}_n(0)=0$ 이다.

 

  Step 4. 모든 $x\in \mathbb{R}$ 에 대해 다음 식이 성립함을 보이자.

$$D{f}_n(x)=f_{n+2}(x)-n{f}_{n+1}(x)$$

  $x\le 0$ 이라면 step 3 에 따라 $D{f}_n(x)=0$ 이므로 위 식이 자명하게 성립한다. $x>0$ 이라고 가정하면 다음이 성립하므로 원하는 결과를 얻는다.

$$\begin{array}{rl}D{f}_n(x)& =\frac{d}{dx}\left(\frac{e^{-\frac{1}{x}}}{x^n}\right)\\ & =\frac{e^{-\frac{1}{x}}\cdot \frac{1}{x^2}\cdot x^n-e^{-\frac{1}{x}}\cdot n{x}^{n-1}}{x^{2n}}\\ & =\frac{e^{-\frac{1}{x}}}{x^{n+2}}-n\frac{e^{-\frac{1}{x}}}{x^{n+1}}\\ & =f_{n+2}(x)-n{f}_{n+1}(x)\end{array}$$

 

  Step 5. 각 $f_n$ 이 $C^{\mathrm{\infty }}$ 급임을 보이자. 귀납법으로 증명하자. Step 4 에 따라 각 $D{f}_n$ 은 두 연속함수의 합성이므로 연속이며, 따라서 각 $f_n$ 은 $C^1$ 급이다. 각 $f_n$ 이 $C^{r-1}$ 급이라고 가정하고 $C^r$ 급임을 보이자. Step 4 와 귀납법 가정에 따라 각 $D{f}_n$ 은 두 $C^{r-1}$ 급 함수의 합성이므로 $C^{r-1}$ 급이며, 따라서 $f_n$ 은 $C^r$ 급이다. (링크의 Thm 3.3 참고) 따라서 원하는 결과를 얻는다.

 

  Step 6. 본 정리를 증명하자. 임의의 $x\in \mathbb{R}$ 에 대해 $f(x)=x{f}_1(x)$ 이므로 $f$ 는 $C^{\mathrm{\infty }}$ 급이다.   $◻$

 

 

 

  Lemma 1.3.  임의의 $Q\in \mathcal{Q}({\mathbb{R}}^n)$ 에 대해 다음을 만족하는 $C^{\mathrm{\infty }}$ 급함수 $\varphi :Q\to \mathbb{R}$ 이 존재한다.$$\{\begin{array}{ll}\varphi (x)>0& \text{if }x\in \text{Int }Q\\ \varphi (x)=0& \text{otherwise}\end{array}$$

 

 

  Proof.  Lem 1.2 의 함수 $f$ 에 대해 함수 $g:\mathbb{R}\to \mathbb{R}$ 를 $g(x)=f(x)f(1-x)$ 라고 정의하면 $g$ 는 $C^{\mathrm{\infty }}$ 급이며 $(0,1)$ 에서 양의 값을 갖고 그 밖에서는 0이다.

 

 

  Rectangle $Q$ 가 다음과 같다고 하자.

$$Q=[a_1,b_1]\times \cdots \times [a_n,b_n]$$

  $\varphi$ 를 다음과 같이 정의하면 주어진 조건을 만족한다.

$$\begin{array}{}◻& \varphi (x_1,\dots ,x_n)=g\left(\frac{x_1-a_1}{b_1-a_1}\right)\cdots g\left(\frac{x_n-a_n}{b_n-a_n}\right)\end{array}$$

 

 

 

  Lemma 1.4.  임의의 $\mathcal{A}\subset {\mathcal{T}}_{{\mathbb{R}}^n}$ 을 생각하자. $\mathcal{A}$ 의 합집합을 $A$ 라고 할때 각 원소가 $A$ 의 부분집합인 어떤 가산모임 $\{Q_1,Q_2,\dots \}\subset \mathcal{Q}({\mathbb{R}}^n)$ 이 존재하여 다음을 만족한다.
  (1) 모임 $\{\text{Int }{Q}_1,\text{Int }{Q}_2,\dots \}$ 는 $A$ 를 덮는다.
  (2) 각 $Q_i$ 는 $\mathcal{A}$ 의 어느 원소의 부분집합이다.
  (3) $A$ 의 각 점은 $\{Q_1,Q_2,\dots \}$ 중 오직 유한개의 원소와만 겹치는 어떤 근방을 갖는다.

 

※ 세 번째 조건은 국소유한조건(local finiteness condition) 이라고 한다. 이는 다른 정리에서도 종종 찾아볼 수 있다.

 

  Proof.  다음의 조건을 만족하는 집합열 $\{D_1,D_2,\dots \}$ 를 생각하자. (존재성은 링크의 Lem 6.2 참고)

 

  1. 각 $D_i$ 는 콤팩트집합이다.

  2. 각 $D_i$ 는 $A$ 의 부분집합이며 $\bigcup _{i=1}^{\mathrm{\infty }}{D}_i$ 가 성립한다.

  3. 각 자연수 $N$ 에 대해 $D_N\subset \text{Int }{D}_{N+1}$ 가 성립한다.

  편의를 위해 $D_{-1},D_0=\varnothing$ 이라고 하자. 각 자연수 $N$ 에 대해 $B_N=D_N\setminus \text{Int }{D}_{N-1}$ 이라고 정의하자. 이때 $B_N$ 은 $D_N$ 과 ${\mathbb{R}}^n\setminus \text{Int }{D}_{N-1}$ 의 교집합이므로 콤팩트하다. 또한 $D_{N-2}\subset \text{Int }{D}_{N-1}$ 이므로 $B_N$ 은 $D_{N-2}$ 와 서로소이다. 따라서 각 $x\in B_N$ 에 대해 $x\in \text{Ext }{D}_{N-2}$ 이므로 어떤 ${\delta }_1>0$ 이 존재하여 $C_{{\delta }_1}^{{\mathbb{R}}^n}(x)$ 가 $\text{Ext }{D}_{N-2}$ 에 속한다. 한편 $x$ 는 $A$ 에 포함되므로 $\mathcal{A}$ 의 어떤 원소에 포함된다. 이때 $\mathcal{A}$ 의 각 원소는 ${\mathbb{R}}^n$ 에서 열려있으므로, 어떤 ${\delta }_2>0$ 이 존재하여 $C_{{\delta }_2}^{{\mathbb{R}}^n}(x)$ 가 $\mathcal{A}$ 의 어떤 원소에 포함된다. $\delta =\text{min}\{{\delta }_1,{\delta }_2\}$ 라고 할때 다음과 같이 집합 $C_x$ 를 정의하면 $C_x$ 는 $C_{\delta }^{{\mathbb{R}}^n}(x)$ 에 포함되므로 $\text{Ext }{D}_{N-2}$ 와 $\mathcal{A}$ 의 어떤 원소에 포함된다.

$$C_x=[x_1-\frac{\delta }{2},x_1+\frac{\delta }{2}]\times \cdots \times [x_n-\frac{\delta }{2},x_n+\frac{\delta }{2}]$$

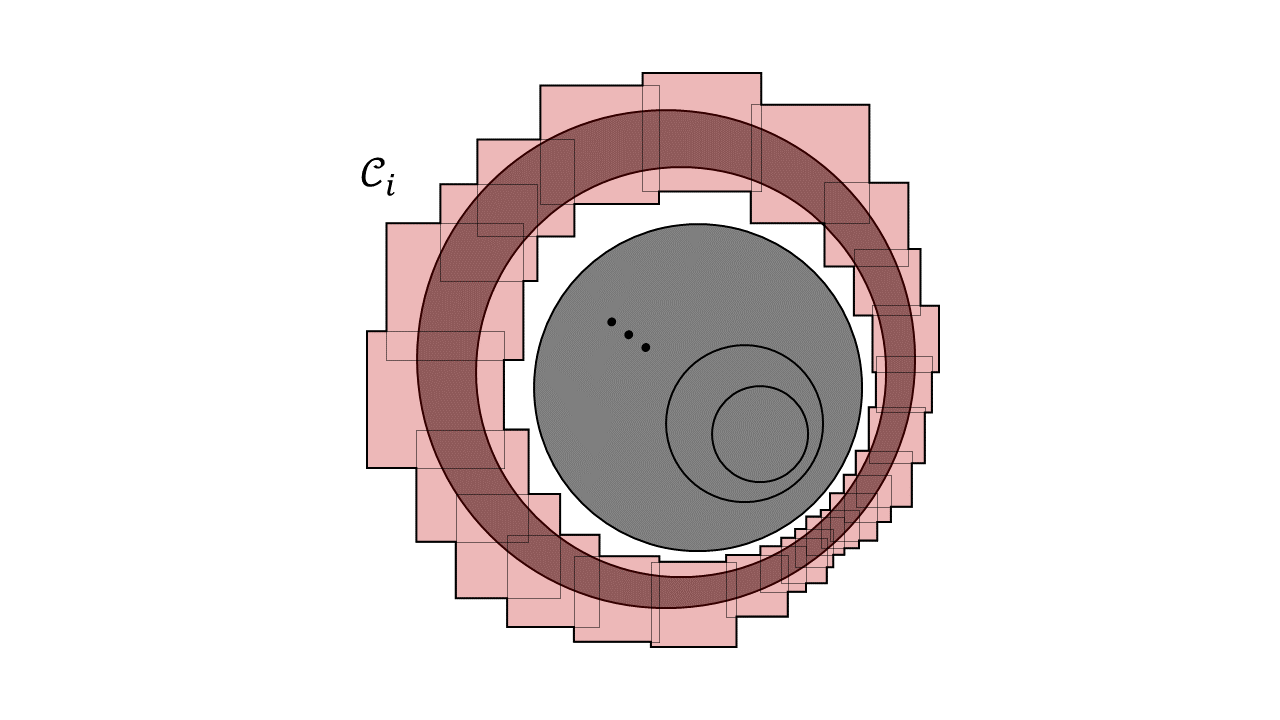
  이때 모임 $\{\text{Int }{C}_x:x\in B_N\}$ 은 콤팩트집합 $B_N$ 을 덮으므로 어떤 유한부분모임 $\{\text{Int }{C}_{x_1},\dots ,\text{Int }{C}_{x_k}\}$ 이 존재하여 $B_N$ 을 다시 덮는다. 이때 ${\mathcal{C}}_N=\{C_{x_1},\dots ,C_{x_k}\}$ 라고 하자. $\mathcal{C}=\bigcup _{i=1}^{\mathrm{\infty }}{\mathcal{C}}_i$ 라고 하면 $\mathcal{C}$ 는 rectangles 의 가산모임이다. (링크의 Thm 2.5 참고) 이때 $\mathcal{C}$ 가 주어진 조건을 만족하는지 확인하자.

 

  (2) 정의에 따라 $\mathcal{C}$ 의 각 원소는 $\mathcal{A}$ 의 어떤 원소의 부분집합이다.

 

  (1) $\mathcal{C}$ 의 각 원소의 interior 의 모임이 $A$ 를 덮음을 확인하자. 각 $x\in A$ 에 대해 $x\in \text{Int }{D}_i$ 를 만족하는 가장 작은 자연수 $i$ 를 선택하자. (이러한 $i$ 의 존재성은 정렬원리에 의해 보장됨) 이때 다음이 성립한다.

$$x\in B_i=D_i\setminus \text{Int }{D}_{i-1}$$

  이때 ${\mathcal{C}}_i$ 에 속하는 rectangles 의 interior 들은 $B_i$ 를 덮으므로, $x$ 는 이 rectangles 중 하나의 interior 에 속한다. 따라서 원하는 결과를 얻는다.

 

  (3) 국소유한조건을 확인하자. 임의의 $x\in A$ 에 대해 어떤 $i$ 가 존재하여 $x\in \text{Int }{D}_i$ 가 성립한다. 이때 모임 ${\mathcal{C}}_{i+2},{\mathcal{C}}_{i+3},\dots$ 에 속하는 rectangles 는 $D_i$ 와 겹치지 않으므로 $\text{Int }{D}_i$ 는 오직 ${\mathcal{C}}_1,\dots ,{\mathcal{C}}_{i+1}$ 에 속하는 몇몇 rectangles 와 겹친다. 이때 $\text{Int }{D}_i$ 는 $x$ 의 근방이며 이는 $\mathcal{C}$ 에 속하는 유한개의 원소와만 겹치므로 원하는 결과를 얻는다.   $◻$

 

 

 

단위분할

 

 

  Definition.  $\varphi :{\mathbb{R}}^n\to \mathbb{R}$ 에 대해 다음의 집합을 $\varphi$ 의 지지집합(support)이라고 한다.$$\text{supp }\varphi =\text{cl}\{x:\varphi (x)\ne 0\}$$  만약 $\text{supp }\varphi$ 가 콤팩트하면 $\varphi$ 가 콤팩트 지지를 갖는다고 하고, $\varphi$ 가 콤팩트 지지함수라고 한다.

 

 

  위 정의에 따르면, $x\notin \text{supp }\varphi$ 일 필요충분조건은 어떤 $U\in {\mathcal{N}}_{{\mathbb{R}}^n}(x)$ 가 존재하여 $U$ 에서 $\varphi$ 가 0인 것이다.

 

 

  Theorem 1.5 (단위분할의 존재성).
  임의의 $\mathcal{A}\subset {\mathcal{T}}_{{\mathbb{R}}^n}$ 과 $\mathcal{A}$ 의 합집합 $A$ 에 대해 다음을 만족하는 ${\mathbb{R}}^n\to \mathbb{R}$ 함수의 가산집합 $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 이 존재한다.
  (1) 모든 $x\in {\mathbb{R}}^n$ 에 대해 ${\varphi }_i(x)\ge 0$ 이다.
  (2) 각 $\text{supp }{\varphi }_i$ 는 $A$ 에 속한다.
  (3) $A$ 의 각 점은 $\{\text{supp }{\varphi }_i{\}}_{i\in \mathbb{N}}$ 중 오직 유한개와 겹치는 근방을 갖는다.
  (4) 모든 $x\in A$ 에 대해 $\sum _{i=1}^{\mathrm{\infty }}{\varphi }_i(x)=1$ 이다.
  (5) 각 ${\varphi }_i$ 는 $C^{\mathrm{\infty }}$ 급이다.
  (6) 각 ${\varphi }_i$ 는 콤팩트 지지를 갖는다.
  (7) 각 $\text{supp }{\varphi }_i$ 는 $\mathcal{A}$ 의 어떤 원소의 부분집합이다.

 

 

  함수의 가산집합 $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 이 위의 몇 조건을 만족하면 다음과 같이 부른다.

 

  (1)~(4): $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 가 $A$ 의 단위분할(partition of unity)이다.

  (5): $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 가 $C^{\mathrm{\infty }}$ 급이다.

  (6): $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 가 콤팩트 지지를 갖는다

  (7): $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 가 $\mathcal{A}$ 에 종속된다.

 

  따라서 이 정리는 임의의 $\mathcal{A}\subset {\mathcal{T}}_{{\mathbb{R}}^n}$ 와 $\mathcal{A}$ 의 합집합 $A$ 에 대해 "$\mathcal{A}$ 에 종속되고 콤팩트 지지를 갖는 $A$ 의 $C^{\mathrm{\infty }}$ 급 단위분할" 이 존재함을 말한다. 오직 단위분할의 존재성 뿐 아니라 여러가지 성질을 갖는 단위분할의 존재성을 검토하는 이유는, 그렇게 하여도 어렵지 않으며 그 자체로 오롯이 단위분할의 존재성을 함의하기 때문이다.

 

 

  Proof.  주어진 $\mathcal{A},A$ 에 대해 Lem 1.4 를 만족하는 가산모임 $\{Q_i{\}}_{i\in \mathbb{N}}\subset \mathcal{Q}({\mathbb{R}}^n)$ 을 생각하자. Lem 1.3 에 따르면 각 $Q_i$ 에 대해 $\text{Int }{Q}_i$ 에서 양의 값을 갖고 그 밖에서는 0인 $C^{\mathrm{\infty }}$ 급함수 ${\psi }_i:{\mathbb{R}}^n\to \mathbb{R}$ 이 존재한다. {조건 (1), (5) 성립} 이때 $\text{supp }{\psi }_i=Q_i$ 이므로 $\text{supp }{\psi }_i$ 는 콤팩트하며, {조건 (6) 성립} Lem 1.4 의 조건에 따라 $\text{supp }{\psi }_i$ 는 $\mathcal{A}$ 의 어떤 원소에 속하고, {조건 (2), (7) 성립} $A$ 의 각 점은 $\{\text{supp }{\psi }_i{\}}_{i\in \mathbb{N}}$ 중 오직 유한개와 겹치는 근방을 갖는다. {조건 (3) 성립} 따라서 $\{{\psi }_i{\}}_{i\in \mathbb{N}}$ 는 (4)를 제외한 모든 조건을 자동으로 만족한다.

 

  (4) 조건 (3)에 따르면 임의의 $x\in A$ 에 대해 $\{{\psi }_i{\}}_{i\in \mathbb{N}}$ 중 오직 유한개를 제외한 모든 함수가 $x$ 에서 0이다. 따라서 다음과 같이 정의한 급수는 모든 $x\in A$ 에서 반드시 수렴한다.

$$\lambda (x)=\sum _{i=1}^{\mathrm{\infty }}{\psi }_i(x)$$

  이때 $\lambda$ 는 임의의 $x\in A$ 의 근방에서 $\{{\psi }_i{\}}_{i\in \mathbb{N}}$ 중 오직 유한개의 함수의 합과 같으므로 $C^{\mathrm{\infty }}$ 급이다. 또한 임의의 $x\in A$ 에 대해 $x$ 를 interior 에 포함하는 rectagle $Q_i$ 가 존재하므로 ${\psi }_i(x)>0$ 이며, 따라서 $\lambda$ 는 양의 값만을 갖는다. 따라서 각 $i$ 에 대해 다음의 함수 ${\varphi }_i:{\mathbb{R}}^n\to \mathbb{R}$ 이 잘 정의된다.

$${\varphi }_i(x)=\frac{{\psi }_i(x)}{\lambda (x)}$$

  이때 $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 는 주어진 조건을 모두 만족한다.   $◻$

 

 

 

  단위분할의 존재성 정리의 조건 (3)인 국소유한조건에 따라 다음의 따름정리를 얻는다.

 

 

  Corollary 1.6.  $A\in {\mathcal{T}}_{{\mathbb{R}}^n}$ 의 단위분할 $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 과 콤팩트집합 $C\subset A$ 에 대해 $C$ 를 포함하는 어떤 $B\in {\mathcal{T}}_{{\mathbb{R}}^n}$ 이 존재하여 $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 중 오직 유한개를 제외한 모든 함수가 $B$ 에서 0이다. 

 

 

  Proof.  각 $x\in C$ 에 대해, 단위분할의 국소유한조건에 따라 어떤 $U_x\in {\mathcal{N}}_{{\mathbb{R}}^n}(x)$ 가 존재하여 $U_x$ 는 $\{\text{supp }{\varphi }_i{\}}_{i\in \mathbb{N}}$ 중 오직 유한개와 겹친다. 이때 $U_x$ 와 겹치는 지지집합의 유한모임을 $\{\text{supp }{\varphi }_i{\}}_{i\in J_x}$ 라고 하자. 이때 $\{{\varphi }_i{\}}_{i\in J_x}$ 를 제외한 $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 의 모든 함수가 $U_x$ 에서 0이다. 모임 $\{U_x:x\in C\}$ 는 $C$ 를 덮으며, $C$ 는 콤팩트하므로 유한부분모임 $\{U_{x_1},\dots ,U_{x_k}\}$ 에 의해 다시 덮인다. 다음과 같이 정의하자.

$$B=\bigcup _{i=1}^k{U}_{x_i}$$

$$J=\bigcup _{i=1}^k{J}_{x_i}$$

  이때 유한모임 $\{{\varphi }_i{\}}_{i\in J}$ 를 제외한 $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 의 모든 함수는 $B$ 에서 0이므로 원하는 결과를 얻는다.   $◻$

 

 

 

단위분할과 적분

 

 

  단위분할은 작은 집합에서 정의되는 성질을 더 큰 집합으로 자연스럽게 확장하는 방법으로 활용되곤 한다. 확장된 의미의 적분가능성도 이러한 방식으로 활용할 수 있다. 다음의 도움정리부터 시작하자.

 

 

  Lemma 1.7.  연속함수 $f:A\in {\mathcal{T}}_{{\mathbb{R}}^n}\to \mathbb{R}$ 가 콤팩트집합 $C\subset A$ 밖에서 0이면 $f$ 는 $A$ 에서 (확장된 의미로) 적분가능하고 $C$ 에서 (원래의 의미로) 적분가능하며 다음이 성립한다.$${}^{\text{ext}}{\int }_{A}f={}^{\text{ord}}{\int }_{C}f$$

 

  ※ 적분가능성의 원래의 의미와 확장된 의미에 대해서는 아래의 두 링크 참고

  [다변수 적분] ch4. 유계집합 위의 적분

  [다변수 적분] ch6. 특이적분

 

  Proof.

  Step 1. $f_C:{\mathbb{R}}^n\to \mathbb{R}$ 이 연속임을 보이자. $\text{Int }A$ ($=A$) 의 임의의 점의 어떤 근방에서 $f_C=f$ 이므로 $f_C$ 는 $\text{Int }A$ 에서 연속이고, $\text{Ext }A$ 의 임의의 점의 어떤 근방에서 $f_C=0$ 이므로 $f_C$ 는  $\text{Ext }A$ 에서 연속이다. 임의의 $x\in \text{Bd }A$ 를 생각하자. $x\notin A$ 이므로 $x\notin C$ 이며, ${\mathbb{R}}^n\setminus C$ 는 열린집합이므로 $x$ 의 어떤 근방에서 $f_C=0$ 이다. 따라서 $f$ 는 $\text{Bd }A$ 에서 연속이며, 정리하면 $f$ 는 ${\mathbb{R}}^n$ 에서 연속이다.

 

  Step 2. $f$ 가 $C$ 에서 (원래의 의미로) 적분가능함을 보이자. 하이네-보렐 정리에 따라 $C$ 는 유계이므로 $C$ 를 포함하는 $Q\in \mathcal{Q}({\mathbb{R}}^n)$ 가 존재한다. $f_C$ 는 ${\mathbb{R}}^n$ 에서 연속이므로 르베그 판정법에 따라 $f_C$ 는 $Q$ 에서 (원래의 의미로) 적분가능하며, 따라서 $f$ 는 $C$ 에서 원래의 의미로 적분가능하다.

 

  Step 3. 이제 본 정리를 증명하자. 링크의 Lem 6.2 의 성질을 만족하는 집합열 $\{C_N{\}}_{N\in \mathbb{N}}$ 을 생각하자. 집합열 $\{\text{Int }{C}_N{\}}_{N\in \mathbb{N}}$ 은 $A$ 를 덮으므로 $C$ 도 덮으며, $C$ 는 콤팩트하므로 이 중 유한모임으로 다시 덮인다. 이 유한모임에서 가장 큰 원소(집합)을 $\text{Int }{C}_M$ 이라고 하자. $C\subset C_M$ 이 성립하며 $C$ 밖에서 $f=0$ 이므로 $M$ 보다 큰 자연수 $N$ 에 대해 다음이 성립한다.

$${}^{\text{ord}}{\int }_{C_N}f={}^{\text{ord}}{\int }_{C}f$$

  이는 함수 $|f|$ 에 대해서도 동일하게 적용되며, 적분의 성질(링크의 Thm 4.3 중 monotonicity)에 따라 ${}^{\text{ord}}{\int }_C|f|$ 는 수열 ${}^{\text{ord}}{\int }_{C_N}|f|$ 의 상한이다. 따라서 링크의 Thm 6.3 에 따라 $f$ 는 $A$ 에서 (확장된 의미로) 적분가능하며 다음이 성립하므로 원하는 결과를 얻는다.

$$\begin{array}{}◻& {}^{\text{ext}}{\int }_{A}f=\underset{N\to \mathrm{\infty }}{lim}{}^{\text{ord}}{\int }_{C_N}f={}^{\text{ord}}{\int }_{C}f\end{array}$$

 

 

 

  위의 도움정리에 따르면, 콤팩트 지지를 갖는 $A$ 의 단위분할 $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 에 대해 ${\varphi }_{i}f$ 는 $\text{supp }{\varphi }_i$ 밖에서 0이므로 ${\varphi }_{i}f$ 는 $A$ 에서 (확장된 의미로) 적분가능하다. 이제 다음의 정리를 확인하자.

 

 

  Theorem 1.8.  연속함수 $f:A\in {\mathcal{T}}_{{\mathbb{R}}^n}\to \mathbb{R}$ 과 콤팩트 지지를 갖는 $A$ 의 단위분할 $\{{\varphi }_i{\}}_{i\in \mathbb{N}}$ 에 대해 $f$ 가 $A$ 에서 (확장된 의미로) 적분가능할 필요충분조건은 다음의 급수가 수렴하는 것이다.$$\sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_i|f|$$  이때 다음이 성립한다.$${}^{\text{ext}}{\int }_{A}f=\sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_{i}f$$

 

 

  Proof.  $A$ 에 속하는 부피를 갖는 모든 콤팩트집합의 모임을 $\mathcal{D}$ 라고 하자.

 

  Step 1. 먼저 $f$ 가 음의 값을 갖지 않을 때 정리가 성립함을 보이자. 이 경우 $|f|=f$ 이다.

 

  ($\Leftarrow$) 급수 $\sum _{i=1}^{\mathrm{\infty }}{}^{\text{ord}}{\int }_{\text{supp }{\varphi }_i}{\varphi }_{i}f$ 가 수렴한다고 하자. 임의의 $D\in \mathcal{D}$ 를 고정하자. Cor 1.6 에 따르면 어떤 자연수 $M$ 에 대해 $i>M$ 이면 $D$ 에서 ${\varphi }_i=0$ 이다. 따라서 임의의 $x\in D$ 에 대해 다음이 성립한다.

$$f(x)=f(x)(\sum _{i=1}^M{\varphi }_i(x))=\sum _{i=1}^M{\varphi }_i(x)f(x)$$

  따라서 다음이 성립한다.

$$\begin{array}{rl}& {}^{\text{ord}}{\int }_{D}f\\ =& {}^{\text{ord}}{\int }_D\sum _{i=1}^M{\varphi }_{i}f\\ =& \sum _{i=1}^M{}^{\text{ord}}{\int }_D{\varphi }_{i}f\text{by linearity}\\ \le & \sum _{i=1}^M{}^{\text{ord}}{\int }_{D\cup (\text{supp }{\varphi }_i)}{\varphi }_{i}f\text{by monotonicity}\end{array}$$

  이때 ${\varphi }_{i}f$ 는 콤팩트집합 $D\cup (\text{supp }{\varphi }_i)\subset A$ 밖에서 0이므로 Lem 1.7 에 따라 다음과 같다.

$${}^{\text{ord}}{\int }_{D\cup (\text{supp }{\varphi }_i)}{\varphi }_{i}f={}^{\text{ext}}{\int }_A{\varphi }_{i}f$$

  따라서 다음을 얻는다.

$$\begin{array}{rl}{}^{\text{ord}}{\int }_{D}f& \le \sum _{i=1}^M{}^{\text{ext}}{\int }_A{\varphi }_{i}f\\ & \le \sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_{i}f\end{array}$$

  $D$ 를 $\mathcal{D}$ 에서 임의로 선택하였으므로 특이적분의 정의에 따라 $f$ 는 $A$ 에서 (확장된 의미로) 적분가능하며 다음을 얻는다.

$${}^{\text{ext}}{\int }_{A}f\le \sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_{i}f$$

 

  ($\Rightarrow$) $f$ 가 $A$ 에서 (확장된 의미로) 적분가능하다고 하자. 링크의 Thm 6.3 에 따르면 링크의 Lem 6.2 의 성질을 만족하는 집합열 $\{C_N{\}}_{N\in \mathbb{N}}$ 에 대해 수열 ${}^{\text{ord}}{\int }_{C_N}f$ 는 위로 유계이다. 이때 모든 $N,i$ 에 대해 적분의 comparison 성질에 따라 다음과 같다.

$${}^{\text{ord}}{\int }_{C_N}{\varphi }_{i}f\le {}^{\text{ord}}{\int }_{C_N}f$$

  따라서 수열 ${}^{\text{ord}}{\int }_{C_N}{\varphi }_{i}f$ 도 위로 유계이다. 그러므로 다시 링크의 Thm 6.3 에 따라 각 ${\varphi }_{i}f$ 는 $A$ 에서 (확장된 의미로) 적분가능하다. 임의의 자연수 $N$ 에 대해 다음이 성립한다.

$$\sum _{i=1}^N{}^{\text{ext}}{\int }_A{\varphi }_{i}f={}^{\text{ext}}{\int }_A\sum _{i=1}^N{\varphi }_{i}f={}^{\text{ext}}{\int }_{A}f$$

  따라서 급수 $\sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_{i}f$ 는 위로 유계이므로 수렴한다. 한편 다음이 성립한다.

$$\sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_{i}f\le {}^{\text{ext}}{\int }_{A}f$$

 

  위의 결과를 종합하면 다음을 얻는다.

$${}^{\text{ext}}{\int }_{A}f=\sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_{i}f$$

 

  Step 2. 일반적인 $f$ 에 대해 본 정리를 증명하자. 링크의 Cor 6.4 에 따르면 $f$ 가 $A$ 에서 (확장된 의미로) 적분가능할 필요충분조건은 $|f|$ 가 $A$ 에서 (확장된 의미로) 적분가능한 것이며, step 1 에 따르면 이는 급수 $\sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_i|f|$ 가 수렴하는 것과 동치이다. 한편 $f=f_{+}-f_{-}$ 이고 $f_{+},f_{-}$ 는 음의 값을 갖지 않으므로 step 1 에 따라 다음이 성립하여 원하는 결과를 얻는다.

$$\begin{array}{rl}& {}^{\text{ext}}{\int }_{A}f\\ =& {}^{\text{ext}}{\int }_A(f_{+}-f_{-})\\ =& {}^{\text{ext}}{\int }_A{f}_{+}-{}^{\text{ext}}{\int }_A{f}_{-}\\ =& \sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_i{f}_{+}-\sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_i{f}_{-}\\ =& \sum _{i=1}^{\mathrm{\infty }}({}^{\text{ext}}{\int }_A{\varphi }_i{f}_{+}-{}^{\text{ext}}{\int }_A{\varphi }_i{f}_{-})\\ ◻& =& \sum _{i=1}^{\mathrm{\infty }}{}^{\text{ext}}{\int }_A{\varphi }_{i}f\end{array}$$

 

 

 

읽어주셔서 감사합니다.

 

 

References)

[1] James R. Munkres. (1991). Analysis on manifolds. CRC press.

---

이전 읽을거리)

[다변수 미분] ch1. 미분의 정의

[다변수 적분] ch1. 적분의 정의

다음 읽을거리: ch2. 미분동형사상